Среднее арифметическое 
является приближенной оценкой истинного значения а измеряемой величины. Поэтому, чтобы эта оценка была наиболее полной, надо обязательно указать, какова погрешность полученного результата D X. Величину абсолютного отклонения среднего из n измерений от истинного значения а называют абсолютной погрешностью или доверительным интервалом среднего. Важно не то, что в результате измерений мы получаем , а важно то, что наряду с должен быть указан интервал D X, в пределах которого где-то находится истинное значение а.
Однако мы не может достоверно утверждать, что истинное значение а окажется внутри интервала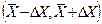 
, мы можем сказать лишь следующее: имеется какая-то вероятность того, что а лежит в пределах этого интервала. Следовательно, доверительный интервал D X необходимо указывать вместе с доверительной вероятностью (надежностью) a попадания истинного значения в пределы этого интервала. Без указания вероятности a сам по себе интервал D Х не может быть принят в качестве оценки погрешности результата.
Если известен вероятностный закон распределения Р (Х), то вероятность попадания истинного значения в пределы этого интервала может быть рассчитана по формуле:
(4)
Расчет показывает, что уже при числе измерений 
выбор погрешности 
, дает величину надежности a, равную 0,68. Другими словами, если взять интервал надежности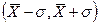 
, то можно утверждать, что в 68 случаях из 100 истинная величина а попадет в указанный интервал, а в 32 случаях из 100 – не попадет в этот интервал.
В случае, когда 
, то a получается равной 0,95. Если 
, a = 0,997, т.е. за пределы доверительного интервала выйдет всего лишь около 3 измерений из 1000.
