Все вещества в соответствии с их способностью проводить электрический ток подразделяются на проводники, диэлектрики и полупроводники. Проводниками называют вещества, в которых электрически заряженные частицы - носители заряда - способны свободно перемещаться по всему объему вещества. К проводникам относятся металлы, растворы солей, кислот и щелочей, расплавленные соли,ионизированные газы.
Ограничим рассмотрение твердыми металлическими проводниками, имеющими кристаллическую структуру. Эксперименты показывают, что при очень малой разности потенциалов, приложенной к проводнику, содержащиеся в нем электроны проводимости, приходят в движение и перемещаются по объему металлов практически свободно.
В отсутствие внешнего электростатического поля электрические поля положительных ионов и электронов проводимости взаимно скомпенсированы, так что напряженность внутреннего результирующего поля равна нулю.При внесении металлического проводника во внешнее электростатическое поле с напряженностью Е0 на ионы и свободные электроны начинают действовать кулоновские силы, направленные в противоположные стороны. Эти силы вызывают смещение заряженных частиц внутри металла, причем в основном смещаются свободные электроны, а положительные ионы, находящиеся в узлах кристаллической решетки, практически не меняют своего положения. В результате внутри проводника возникает электрическое поле с напряженностью Е'.
Смещение заряженных частиц внутри проводника прекращается тогда, когда суммарная напряженность поля Е в проводнике, равная сумме напряженностей внешнего и внутреннего полей, станет равной нулю:
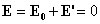
Представим выражение, связывающее напряженность и потенциал электростатического поля, в следующем виде:
где Е - напряженность результирующего поля внутри проводника; n - внутренняя нормаль к поверхности проводника. Из равенства нулю результирующей напряженности Е следует, что в пределах объема проводника потенциал имеет одно и то же значение: 
.
Полученные результаты позволяют сделать три важных вывода:
1. Во всех точках внутри проводника напряженность поля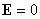 
, т. е. весь объем проводника эквипотенциален.
2. При статическом распределении зарядов по проводнику вектор напряженности Е на его поверхности должен быть направлен по нормали к поверхности 
, в противном случае под действием касательной к поверхности проводника компоненты напряженности 
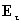заряды должны перемещаться по проводнику.
3. Поверхность проводника также эквипотенциальна, так как для любой точки поверхности
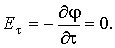
Если проводнику сообщить избыточный заряд, то этот заряд распределится по поверхности проводника. Действительно, если внутри проводника выделить произвольную замкнутую поверхность S, то поток вектора напряженности электрического поля через эту поверхность должен быть равен нулю. В противном случае внутри проводника будет существовать электрическое поле, что приведет к перемещению зарядов. Следовательно, для того, чтобы выполнялось условие
,
суммарный электрический заряд внутри этой произвольной поверхности должен равняться нулю.
Напряженность электрического поля вблизи поверхности заряженного проводника можно определить, используя теорему Гаусса. Для этого выделим на поверхности проводника малую произвольную площадку d S и, считая ее за основание, построим на ней цилиндр с образующей d l (рис. 3.1). На поверхности проводника вектор Е направлен по нормали к этой поверхности. Поэтому поток вектора Е через боковую поверхность цилиндра из-за малости d l равен нулю. Поток этого вектора через нижнее основание цилиндра, находящееся внутри проводника, также равен нулю, так как внутри проводника электрическое поле отсутствует. Следовательно, поток вектора Е через всю поверхность цилиндра равен потоку через его верхнее основание d S':
,
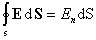где Еn - проекция вектора напряженности электрического поля на внешнюю нормаль n к площадке d S.
По теореме Гаусса, этот поток равен алгебраической сумме электрических зарядов, охватываемых поверхностью цилиндра, отнесенной к произведению электрической постоянной и относительной диэлектрической проницаемости среды, окружающей проводник. Внутри цилиндра находится заряд 
, где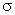 
- поверхностная плотность зарядов. Следовательно 
и 
, т. е. напряженность электрического поля вблизи поверхности заряженного проводника прямо пропорциональна поверхностной плотности электрических зарядов, находящихся на этой поверхности.
Экспериментальные исследования распределения избыточных зарядов на проводниках различной формы показали, что распределение зарядов на внешней поверхности проводника зависит только от формы поверхности: чем больше кривизна поверхности (чем меньше радиус кривизны), тем больше поверхностная плотность заряда.
Вблизи участков с малыми радиусами кривизны, особенно около острия, из-за высоких значений напряженности происходит ионизация газа, например, воздуха. В результате одноименные с зарядом проводника ионы движутся в направлении от поверхности проводника, а ионы противоположного знака к поверхности проводника, что приводит к уменьшению заряда проводника. Это явление получило название стекания заряда.
На внутренних поверхностях замкнутых полых проводников избыточные заряды отсутствуют.
Если заряженный проводник привести в соприкосновение с внешней поверхностью незаряженного проводника, то заряд будет перераспределяться между проводниками до тех пор, пока их потенциалы не станут равными.
Если же тот же заряженный проводник касается внутренней поверхности полого проводника, то заряд передается полому проводнику полностью.
Эта особенность полых проводников была использована американским физиком Робертом Ван-де-Граафом для создания в 1931 г. электростатического генератора, в котором высокое постоянное напряжение создается посредством механического переноса электрических зарядов. Наиболее совершенные электростатические генераторы позволяют получать напряжение величиной до 15 - 20 МВ.
В заключение отметим еще одно явление, присущее только проводникам. Если незаряженный проводник поместить во внешнее электрическое поле, то его противоположные части в направлении поля будут иметь заряды противоположных знаков. Если, не снимая внешнего поля, проводник разделить, то разделенные части будут иметь разноименные заряды. Это явление получило название электростатической индукции.
10 вопрос Электроемкость.
Рассмотрим уединенный проводник, т. е. проводник, находящийся в однородной изотропной среде вдали от других проводников и заряженных тел. При сообщении такому проводнику избыточного заряда q последний распределяется по поверхности проводника с поверхностной плотностью 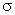, которая зависит от размеров и формы проводника.
Выделим на поверхности проводника малый элемент площади d S, полагая, что заряд этого элемента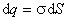 
является точечным. В другой точке поверхности этого же проводника, отстоящей от элемента d S на расстояние r, этот заряд создает электрическое поле, потенциал которого равен
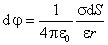
,где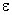 
- относительная диэлектрическая проницаемость среды, в которой находится проводник. Интегрируя это выражение по всей поверхности проводника S, найдем потенциал, создаваемый в рассматриваемой точке всем проводником:
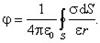
Так как в различных точках на поверхности проводника поверхностная плотность заряда имеет разные значения, то будем полагать, что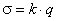 
, где k - некоторая функция координат выбранного элемента поверхности d S. Тогда выражение для потенциала проводника имеет вид
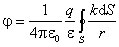. (3.1)
В полученном выражении интеграл 
зависит от размеров и формы поверхности проводника, а также от расположения точки, для которой определяется потенциал.
Значения этого интеграла не зависят от величины заряда, сообщенного проводнику, т. е. одинаковы при различных значениях заряда q.
Из формулы (3.1) следует, что потенциал уединенного проводника прямо пропорционален его заряду и отношение заряда q к потенциалу 
для данного проводника есть величина постоянная. Это отношение называется электрической емкостью, или электроемкостью, проводника:
Электрическая емкость уединенного проводника зависит от его формы и размеров, а также от величины относительной диэлектрической проницаемости среды, в которой он находится. Электроемкость не зависит от материала проводника, его агрегатного состояния, от формы и размеров возможных полостей внутри проводника. Электроемкость не зависит также ни от заряда проводника, ни от его потенциала.
В качестве примера найдем электроемкость уединенного проводящего шара радиуса R, покрытого слоем диэлектрика с относительной проницаемостью 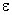и толщиной d. Пусть шар имеет заряд q. Тогда напряженность поля, создаваемого шаром внутри диэлектрического слоя,
За пределами слоя напряженность поля определяется выражением:
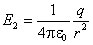
Потенциал поверхности шара:
Таким образом, электроемкость шара, покрытого слоем диэлектрика, есть
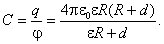
В случае, если толщина диэлектрического слоя 
, емкость шара равна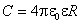 
. При d =0 она равна 
.
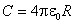Из приведенных соотношений следует, что потенциалы одинаково заряженных и геометрически подобных проводников должны быть обратно пропорциональны их линейным размерам, а их электрические емкости прямо пропорциональны этим размерам.
Электроемкость проводника численно равна заряду, который нужно сообщить этому проводнику для изменения его потенциала на единицу. В СИ единица измерения электрической емкости 1 фарада (Ф). Это емкость такого проводника, потенциал которого изменяется на 1 В при сообщении ему заряда в 1 Кл: 1 Ф = 1 Кл / 1 В.
Если вблизи проводника есть другие проводящие незаряженные тела, то при сообщении проводнику некоторого электрического заряда его потенциал будет меньше, чем потенциал уединенного проводника таких же формы и размеров. Это обусловлено тем, что на поверхностях тел, обращенных к заряженному проводнику, будут индуцироваться электрические заряды противоположного знака.
Для наглядности поясним это явление на примере. Пусть на некотором расстоянии от проводящего шара радиуса R расположен незаряженный металлический стержень длиной l так, что его ближний конец находится на расстоянии r от центра шара, а дальний - на расстоянии (r + l). Если шару сообщить положительный электрический заряд Q, то создаваемое шаром поле будет индуцировать на ближнем конце стержня заряд -q, а на дальнем заряд + q. Потенциал шара при этом будет равен
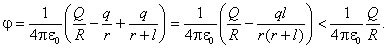
Следовательно, электроемкость проводника возрастает, если недалеко от него находятся другие проводящие тела. В этом случае принято говорить о взаимной электроемкости проводников.
Наибольший интерес представляет взаимная электроемкость системы из двух проводников с равными по величине и противоположными по знаку электрическими зарядами: |+ q | = |- q | = q. Их взаимная электрическая емкость определяется как отношение заряда к разности потенциалов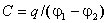 
,где 
разность потенциалов между проводниками.
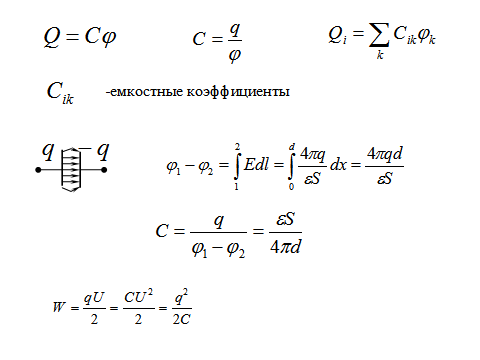с обзорки
