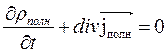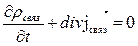Общее определение

ПЛО́ТНОСТЬ ТО́КА, векторная характеристика электрического тока j, равная по модулю электрическому заряду, проходящему за единицу времени через единичную площадку, перпендикулярную направлению упорядоченного движения заряженных частиц.

При равномерном распределении плотности электрического тока по сечению проводника плотность тока j будет равна отношению силы тока I в нем к площади его поперечного сечения S:

j = I/ S

Плотность тока характеризует силу тока, проходящего через единицу площади поперечного сечения проводника, перпендикулярного направлению тока

Единицей измерения плотности тока является А/м².

Плотность тока можно определить также следующим образом:

Так как сила тока I = nevS, где:

n — концентрация носителей заряда;

e — заряд носителей тока;

v — средняя скорость упорядоченного движения частиц;

S — площадь поперечного сечения проводника, через который течет ток,

То плотность тока J = I/ S = nev S/ S = nev.

Произведение ne характеризует плотность заряда е (заряд в единице объема), поэтому плотность электрического тока:

j =r_еv.

Плотность тока величина векторная, по направлению совпадает с направлением вектора скорости v, т. е. с направлением упорядоченного движения электрических зарядов.

Плотность тока пропорциональна вектору напряженности:

j = sЕ.

Коэффициент пропорциональности — проводимость вещества проводника.

Плотность тока более фундаментальная характеристика, чем сила тока, так как дает информацию о распределении течения заряда по проводнику.

 

 

4. Закон сохранения заряда.

Зако́н сохране́ния электри́ческого заря́да гласит, что алгебраическая сумма зарядов электрически замкнутой системы сохраняется.Закон сохранения заряда выполняется абсолютно точно. Запишем закон сохранения электрического заряда 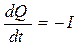для некоторого объема V, окруженного замкнутой поверхностью S (рис. 2.2). В этом случае (3*) и теорема Гаусса- Остроградского дают

.

 

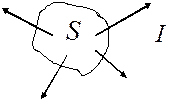
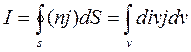Рис. 2.2

В предположении, что поверхность S не изменяется со временем, 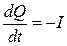примет вид

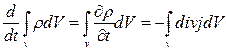
Так как объем V выбран произвольно, то

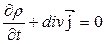
Так выражается закон сохранения электрического заряда в дифференциальной форме.

Сохраняя обозначения и 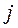для плотностей свободных зарядов и токов, полные плотности, очевидно, можно представить в виде

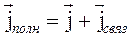
В большинстве электродинамических задач предполагается, что закон сохранения имеет место, как для свободных, так и для связанных зарядов в отдельности, т. е. исключаются процессы перехода связанных зарядов в свободные и обратно. Поэтому разумно принять, что