В макроскопической теории отношение 
является вполне определенной функцией точки r и называется плотностью электрического заряда 
. Таким образом,
При этом заряд в произвольной области V представляется в виде
Введем теперь еще одно важное понятие - плотности электрического тока j. Для этого рассмотрим площадку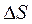 
с нормалью n (рис. 2.1) и подчитаем заряд 
, пересекший ее за промежуток времени 
. Выделим сначала заряды еi, имеющие скорости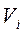 
, лежащие в некотором интервале 
со средней скоростью V. Тогда все такие заряды, находящиеся в объеме призмы с высотой 
и основанием 
, пройдут за время 
через площадку . Учитывая, что плотность выделенных электрических зарядов равна
,
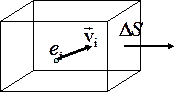
находим заряд, пересекший площадку 
Рис. 2.1
за отрезок времени 
со средней скоростью v:
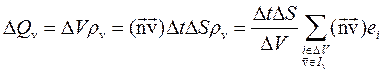
Теперь, чтобы найти полный заряд 
, достаточно лишь просуммировать 
по всем возможным интервалам 
:
где введена плотность электрического тока
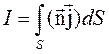(2.1)
