Рассмотрим произвольную ограниченную систему зарядов находящихся диэлектрической среде. Выделим произвольную область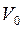 
содержащую систему зарядов и ограниченную замкнутой поверхностью S. Энергия электростатического поля, содержащаяся в V0 равна
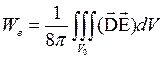
Пологая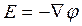 
и интегрируя по частям, находим
(19.1)
Будем считать поверхность S сферой бесконечно большого радиуса R. Тогда при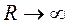 
потенциал 
убывает как 
, где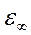 
- диэлектрическая проницаемость среды на бесконечности, а 
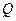- полный свободный заряд системы, равный по теореме Гаусса
Все это позволяет получить следующую оценку для поверхностного интеграла (19.1):
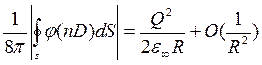
Так как потенциал убывает обратно пропорционально расстоянию то при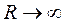 
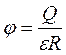
(19.2)
где 
-область занятое свободными зарядами.
Учтем теперь, что потенциал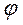 
удовлетворяет уравнению Пуассона 
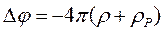и поэтому может быть записан в форме
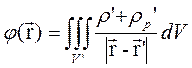(19.3)
где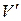 
- область, занятая свободными и связанными зарядами. Подставляя (19.3) в (19.2), получаем выражение для энергии электростатического поля в среде:
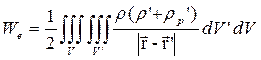
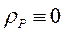обычно используемое симметричное выражение 
(19.4)
Если заряды считать точечными, то (19. 4) будет содержать расходящиеся интегралы, отвечающие собственным энергиям отдельных зарядов. Если заряд е равномерно распределен по поверхности шарика радиуса а, то энергия электростатического поля, равна
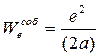
и при 
оказывается бесконечной.
Энергия системы точечных зарядов будет равна, здесь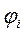 
- потенциал создаваемый всеми зарядами кроме i-го.
