Рассмотрим систему токов, погруженную в магнитик с проницаемостью 
. Выделим область V0 ограниченную поверхностью S. Энергия магнитного поля, содержащаяся в V0 равна
Пологая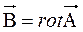 
и применяя теорему Гаусса - Остроградского, с учетом тождества 
находим
(21.1)
Для ограниченной системы токов, асимптотическое поведение вектора- потенциала А при 
имеет вид
где m- полный магнитный момент системы.
Таким образом, при 
поверхностный интеграл в (21.1) исчезает и выражение для энергии магнитного поля с учетом уравнения 
принимает вид
где V -область занятая токами проводимости.
Поле В создается как токами проводимости, так и токами намагничения, можно записать следующее уравнение для векторного потенциала А:
Магнитное поле создается как токами проводимости 
так и токами намагничение 
и вектор 
удовлетворяет уравнению типа Пуассона выражения для векторного потенциала можно записать:
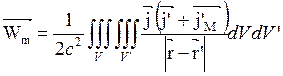
- область занятая токами проводимости и намагничения.
Для однородного магнетика с постоянной проницаемостью 
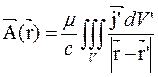
упрощается:
Токи текут по проводникам, занимающим некоторые области 
В то же время из условия стационарности токов 
вытекает, что линии тока являются замкнутыми. Выделяя области 
, отвечающие полным током силой 
, очевидно, можно положить 
и переписать в виде:
где введены коэффициенты
Называемые взаимной индуктивностью при 
и индуктивностью при 
.
Для квазилинейных проводников подстановкой 
каждый объемный интеграл сводится к линейному:
Однако такое упрощение допустимо только при вычислении взаимной индуктивности 
непересекающихся квазилинейных проводников, когда 
.
