1. Найти область определения
2. Найти производную функции
3. Найти критические точки (приравнять производную к 0, найти точки, в которых
производная равна нулю или не существует)
4. Разбить область определения критическими точками на промежутки
5. Определить знак производной на каждом из промежутков
6. Сделать выводы о возрастании и убывании функции на этих промежутках.
Пример
Найти интервалы монотонности (возрастания и убывания) функции  .
.
Найдём область определения 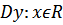
Найдём производную
 Отсюда х=0,х=1, х=-1
Отсюда х=0,х=1, х=-1
Разобьём область определения критическими точками на промежутки и определим знак производной на каждом из промежутков.
 |
Ответ:  (-∞, -1)
(-∞, -1)  (0,1)
(0,1)
 (-1,0)
(-1,0)  (1,+∞)
(1,+∞)
Точка х0 называется точкой локального максимума, если существует такая окрестность х0, что для всех х из этой окрестности выполняется  .
.
Точка х0 называется точкой локального минимума, если существует такая окрестность х0, что для всех х из этой окрестности выполняется  .
.

х0 х х0 х
максимум минимум
Если в точке х0 из области определения производная функции меняет знак с «+» на «-», то в этой точке функция достигает локального максимума.
Если в точке х0 из области определения производная функции меняет знак с
«-» на «+», то в этой точке функция достигает локального минимума.
Таким образом функция может достигать максимума и минимума лишь в критических точках.
Точки локального максимума и минимума называются точками экстремума.
Схема исследования на экстремумы функции такая же как и схема исследования на возрастание и убывание, только необходимо сделать выводы об экстремумах.






