Пусть s (t)- закондвижения, v(t) - функция скорости, а(t) - функция ускорения. Тогда 
,
т.е. производная от закона движения есть скорость.
Таблица производных
| 
|
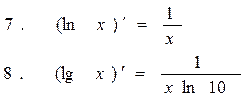
Для нахождения производных нет необходимости каждый раз применять определение, достаточно знать таблицу производных, например 
. Эту производную мы получили по 3 пункту таблицы, приняв n=3.
Свойства производной
1. Производная суммы равна сумме производных
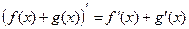
Пример
Найти производную функции y = x2 − 5x.
Решение
2. Производная произведения равна сумме произведений производной одного множителя на другой
Пример
Найти производную функции 
Решение
3. Постоянный коэффициент можно выносить за знак производной
Пример
Найти производную функции 2√x − 3sin x
