Пусть переменная y является функцией от переменной u (
), а переменная u в свою очередь является функцией от независимой переменной х 
, тесть задана сложная функция 
.
Правило. Если 
- функции, имеющие производные, то производная сложной функции равна производной данной функции 
по промежуточному аргументу и и умноженной на производную самого промежуточного аргумента 
по независимой переменной х, т.е
Тогда таблица производных для сложных функций будет выглядеть
Пример
а) 
.
Функцию представим в виде 
, где 
.
Тогда на основании дифференцирования сложной функции
;
б) 
Пусть 
, тогда .
, тоді 
.
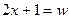, тоді 
.
Обычно при дифференцировании сложную функцию не раскладывают на простые, а дифференцируют таким образом
.
4. Алгоритм составления уравнения касательной к графику функции y = f(x)
1. Обозначить буквой х0 абсциссу точки касания.
2. Найти f(х0).
3. Найти f '(x) и f '(х0).
4. Подставить найденные числа х0, f(х0), f '(х0) в общее уравнение касательной
y - f(х0) = f '(х0)(x – х0).
Пример. Составьте уравнение касательной в точке M(3; – 2) к графику функции
