Производная и ее применение
Понятие производной
Пусть дана функция y=f(x). Если выбрать некоторое значение аргумента х. то соответствующее ему значение функции называют начальным. Прибавим к начальному значению аргумента некоторое его приращение 
, получим х+ , тогда f(х+ ) будет наращенное значение функции. 
называется приращением функции.
y y=f(x)
f(х+ ) 
f(x)
x х+ x
Определение: Производной 
от функции f(x) называется предел отношения приращения функции к приращению аргумента при 
, т.е.
.
Нахождение производной функции называется дифференцированием. Операция дифференцирования обозначается штрихом, например: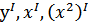 
.
Геометрический смысл производной
Поясним геометрический смысл производной, рассмотрим рис 1. Из треугольника MM 1 N получается, что угловой коэффициент секущей или тангенс угла её наклона к оси ОХ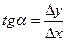 
. Устремим теперь ∆ х к нулю. При этом точка М1 перемещается по кривой и приближается к точке М. В предельном положении хорда ММ1 станет касательной МТ. Обозначим угол, образованный касательной с положительным направлением оси ОХ через φ.
Таким образом значение производной в некоторой точке равно угловому коэффициенту (тангенс угла наклона к оси ОХ) касательной в этой точке, проведенной к графику функции, т.е.
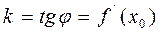(рис 2)
Найдем уравнение касательной к графику функции в точке М0(х0;y0).
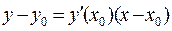- уравнение касательной к графику функции в точке х0,
где у0=у(х0)
Рис 1
Рис 2
