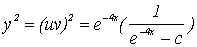Однородным дифференциальным уравнением первого порядка, называется уравнение, имеющее вид
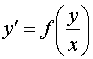(7)
Подстановка 
; 
; 
, где 
преобразует это уравнение к уравнению с разделяющимися переменными.
,
,
.
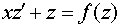2. 4. Линейные уравнения первого порядка и уравнения Бернулли
Дифференциальное уравнение первого порядка называется линейным, если оно содержит 
и 
в первой степени, то есть имеет вид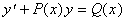 
.
Уравнением Бернулли называется дифференциальное уравнение первого порядка вида 
, где 
и 
.
Эти уравнения решают с помощью подстановки 
.
Пример 3. Решить уравнение 
.
Решение. Это уравнение является уравнением Бернулли. Решим это уравнение с помощью подстановки . Тогда 
. Подставляя и в уравнение, получим: 
. Преобразуем это уравнение к виду 
. Найдем функцию 
, полагая в последнем уравнении 
. Тогда 
(мы нашли одну из первообразных функции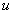 
). Подставляя найденную функцию в уравнение относительно 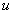и 
, получим 
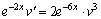или 
.
Разделяем переменные и находим функцию :
Возведя 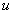в квадрат, находим
