1. Знайти диференціал функції f:
а) 
; б) 
, в) 
.
Розв’язання. Для знаходження диференціала функції використаємо формулу df (х)= 
.
а) 
;
б)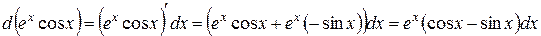 
;
в) 
.
2. Обчислити наближено:
а) 
; б) 
; в) 
; г) 
.
Розв’язання. а) Для знаходження наближеного значення виразу використаємо формулу (4.8):
= 
.
б) Використаємо формулу (4.9):
= 
= 
» 
=
=5, 0012.
в) Використовуючи формулу (4.7) для наближених обчислень, одержимо:
.
Покладемо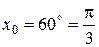 
. Тоді 
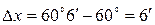або в радіанах 
.
Отже,
= 
= 
» 
= 
.
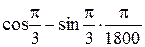Будемо обчислювати з точністю до четвертого десяткового знаку. Оскільки 
, 
, то
» 
.
г) За формулою (4.7) маємо:
.
Тоді
.
3. Знайти похідну другого порядку функції f:
а) 
; б) 
; в) 
.
Розв’язання. Знайдемо послідовно першу, а потім другу похідну:
а) 
; 
.
б) 
;
.
в) 
;
=
= 
= 
.
4. Знайти похідну n -го порядку функції 
.
Розв’язання. Послідовно знаходимо:
;
;
;
;
.
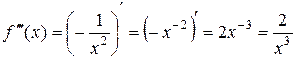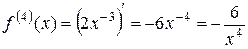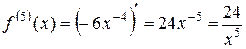Аналізуючи знайдені похідні, можна висунути припущення про те, що
.
Це припущення можна довести, використовуючи метод математичної індукції.
5. Для функції 
знайти 
.
Розв’язання. Послідовно знаходимо:
;
;
;
.
Тоді за формулою (4.10) маємо:
= 
.
Завдання для самостійного розв’язування
8. Знайти диференціал функції f:
а) 
; б) 
; в) 
;
9. Не користуючись калькулятором, обчислити наближено:
а) 
; б) 
; в) 
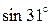; г) 
.
10. Для заданої функції знайти похідну вказаного порядку:
а) 
; б) 
; в) 
;
Відповіді:
8. а) 
; б) 
; в) 
.
9. а) 1,2; б) 2,0004; в) 0,5151; г) –0,04.
10. а) 
; б) 
; в) 
;
