1. 
.
2. 
.
3. 
.
4. Якщо z = f (х), х = g (t), тобто 
, то 
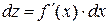. Отже, форма диференціала не залежить від того, чи є аргумент x незалежною змінною, чи функцією іншого аргументу. Таку властивість називають інваріантністю форми диференціала.
Нехай у точці х 0 існує 
. Якщо у точці х 0 також існує похідна функції 
, тобто існує 
, то її називають другою похідною або похідною другого порядку функції f у точці х 0 і позначають 
або 
. Аналогічно означають похідні третього, четвертого і т.д. порядків.
Другим диференціалом або диференціалом другого порядку в точці х 0 функції y = f (x), двічі диференційовної в цій точці, називають диференціал від диференціала першого порядку і позначають 
, тобто
= 
.
Справедлива рівність = 
.
Аналогічно для функції y = f (x), n разів диференційовної в точці х 0, вводять поняття диференціала n -го порядку: 
= 
. При цьому є справедливою рівність
= 
. (4.10)
