Нехай функція y = f (x) диференційована в точці х 0. Похідна функції f у точці х 0 визначається рівністю
 . (4.1)
. (4.1)
Оскільки 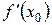 – це
– це 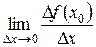 , то
, то  відрізняється від
відрізняється від  на деяку нескінченно малу величину
на деяку нескінченно малу величину  , яка прямує до нуля, коли
, яка прямує до нуля, коли 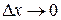 . Тому рівність (4.1) можна записати у вигляді
. Тому рівність (4.1) можна записати у вигляді
 =
= 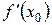 +
+  , (4.2)
, (4.2)
де  , коли
, коли 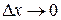 .
.
З (4.2) маємо
 . (4.3)
. (4.3)
Обидва доданки у рівності (4.3) є нескінченно малими величинами при 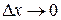 .
.
Якщо функція y = f (x) диференційовна у точці х 0, то добуток  називають диференціалом функції f у точці х 0 і позначають df (х 0).
називають диференціалом функції f у точці х 0 і позначають df (х 0).
Отже,
df (х 0)=  . (4.4)
. (4.4)
Тому рівність (4.3) можна записати так:
 . (4.5)
. (4.5)
Якщо f (x)= x, то  . Отже,
. Отже,  . Враховуючи це, рівність (4.4) можна записати у вигляді
. Враховуючи це, рівність (4.4) можна записати у вигляді
df (х 0)=  . (4.6)
. (4.6)
З рівності (4.5) випливає, що приріст функції відрізняється від диференціала на нескінченну малу величину при 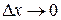 . Тому
. Тому
 або
або  або
або
 , коли
, коли  . (4.7)
. (4.7)
За допомогою формули (4.7) можна обчислювати наближені значення функції у точках, близьких х 0.
Використовуючи формулу (4.7) можна довести, що
 . (4.8)
. (4.8)
Зокрема, якщо  , то
, то
 . (4.9)
. (4.9)






