Похідна функції.
Нехай функція y = f (x) визначена в деякому околі точки х 0. Надамо х 0 приросту D х і розглянемо відповідний приріст функції D f (x 0)= f (x 0+D х)– f (x 0).
Похідною функції y = f (x) у точці х 0 називають границю відношення приросту D f (x 0) функції до приросту D х аргументу, коли приріст аргументу D х прямує до нуля. Позначають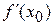 
або 
.
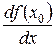Отже, за означенням: =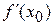 
.
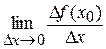Якщо 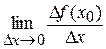=¥, то кажуть, що функції f у точці х 0 має нескінченну похідну.
Для знаходження похідної функції f у точці х 0 за означенням потрібно виконати такі кроки:
1. Надати аргументу х 0 приросту D х і знайти відповідний приріст функції D f (x 0)= f (x 0+D х)– f (x 0).
2. Скласти відношення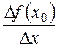 
.
3. Знайти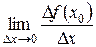 
. Якщо ця границя існує, то вона є похідною функції f у точці х 0, тобто = .
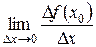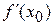Нехай функція y = f (x) визначена на півінтервалі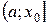 
(на піввідрізку 
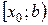). Вважають, що функція f у точці х 0 має ліву (праву) похідну, якщо в цій точці існує ліва (права) границя:
.
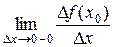
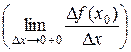Для того щоб у точці х 0 існувала похідна 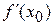, необхідно й достатньо, щоб у цій точці існувала ліва і права похідні цієї функції і щоб ліва похідна дорівнювала правій похідній.
Функцію, що має скінченну похідну в точці х 0, називають диференційовною в цій точці. Якщо функція диференційовна в точці х 0, то вона є неперервною в цій точці.
Нехай D 1 – множина точок, у яких функція f диференційовна. Поставивши у відповідність кожному числу х Î D 1 число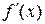 
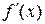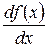, одержимо нову функцію з областю визначення D 1. Цю функцію називають похідною функції y = f (x) і позначають або 
, або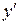 
.
Операцію відшукання похідної функції називають диференціюванням функції.
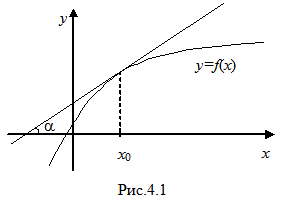Геометричний зміст похідної: 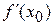дорівнює кутовому коефіцієнту k дотичної, проведеної до графіка функції f у точці з абсцисою х 0, тобто 
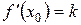=tg a, де a – кут між дотичною і додатним напрямом осі абсцис (рис.4.1).
Існування похідної функції f у точці х 0 рівносильне існуванню дотичної, проведеної до графіка функції f у точці з абсцисою х 0.
Рівняння дотичної, проведеної до графіка функції f у точці з абсцисою х 0: 
.
Механічний зміст похідної: якщо матеріальна точка рухається за законом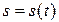 
, то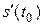 
дорівнює швидкості точки в момент часу 
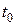, тобто 
; якщо матеріальна точка рухається із швидкістю, що змінюється за законом 
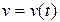, то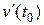 
дорівнює прискоренню точки в момент часу 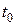, тобто 
.
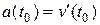Економічний зміст похідної: якщо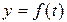 
– кількість виробленої виробником продукції за час t, то 
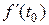дорівнює продуктивності праці виробника в момент часу 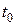, тобто 
.
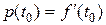