4-тензоры, четырёхте́нзоры — класс математических объектов, используемый для описания некоторых физических полей в релятивистской физике, тензор, определённый на четырёхмерном пространстве-времени[1].
Замечание: в литературе 4-тензоры часто называются просто тензорами, а размерность и природа векторного пространства (многообразия), на котором они заданы в этом случае оговариваются явно или очевидны из контекста.
В общем случае 4-тензор является объектом с набором индексов:
причём каждый из индексов принимает четыре значения (обычно от нуля до трёх или от одного до четырёх, то есть 
итд.
При смене системы отсчёта компоненты этого объекта преобразуются так:
,
где 
— матрица поворота в четырёхмерном пространстве-времени (матрица группы Лоренца), а 
— обратная ей.
Верхние индексы называются контравариантными, а нижние — ковариантными. Суммарное число индексов задаёт ранг тензора. 4-вектор является 4-тензором первого ранга.
Обычно в физике тензоры одинаковой природы с разным числом ковариантных и контравариантных индексов считаются различными представлениями одного и того же объекта. Опускание или поднимание индекса проводится с помощью метрического тензора 
, например для 4-тензора второго ранга
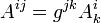
Алгебра внешнего произведения позволяет также вводить для антисимметричных тензоров родственные им дуальные тензоры.
Уравнения теории относительности, электродинамики, и многих современных фундаментальных теорий, включающих их, особенно удобно записывать, используя 4-векторы и 4-тензоры. Главным преимуществом такой записи есть то, что в этой форме уравнения автоматически лоренц-инвариантны, то есть не изменяются при переходе от одной инерциальной системы координат к другой.
Соответствующий 4-тензор существует также и для описания электромагнитного поля. Это 4-тензор второго ранга. При его использовании основные уравнения для электромагнитного поля: уравнение Максвелла и уравнение движения заряженной частицы в поле имеют особенно простую и элегантную форму.
