Введение мультипольного момента основано на довольно простых соображениях, к-рые удобно проиллюстрировать на примере статич. электрич. полей, создаваемых системой точечных зарядов ei. B системе координат с центром, расположенным где-нибудь внутри системы зарядов, положения зарядов характеризуются радиус-векторами r i(i - номер заряда). Потенциал этой системы зарядов в точке R определяется суммой потенциалов всех частиц:
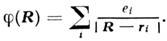
Если интересующая нас точка R значительно удалена от системы зарядов, т. е. | r i |/| R | << 1, то потенциал можно разложить в Тейлора ряд по степеням этого отношения:
где a j = 1, 2, 3 - нумеруют компоненты соответствующих векторов; по повторяющимся a j производится суммирование. Такое разложение потенциала наз. разложением по M. или мультипольным разложением. В нулевом приближении
т. е. f(0) совпадает с потенциалом точечного заряда q, равного суммарному заряду системы. Величина 
- мультипольный момент нулевого порядка - полностью определяет в этом приближении потенциал поля на больших расстояниях. Следующий член разложения
Здесь n - единичный вектор, направленный вдоль R. Величина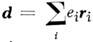 
, определяющая (если q = 0) потенциал в 1-м порядке, наз. динольным моментом системы зарядов или мультипольным моментом 1-го порядка. T. о., характеризуя потенциал (или поле) в 1-м порядке, можно заменить систему зарядов точечным зарядом q и диполем с дипольным моментом d. След. член разложения f(2) после нек-рых преобразований записывается в виде
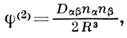
где 
(или Q ab = D ab/6) наз. квадрупольным моментом системы зарядов (dab - Кро-некера символ).
Общий член разложения потенциала определяется неприводимым тензором l -го ранга
к-рый наз. 2 l -польным моментом системы зарядов, l - порядок M. Тензор 2 l -польного момента симметричен по всем индексам и обращается в нуль при сво-рачивании по любой паре индексов. Общий член разложения потенциала имеет более компактную форму при разложении j(R) по сферическим функциям:
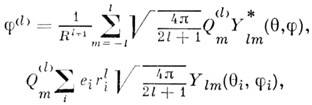
где Ylm, Y*lm - сферич. ф-ции, q, f и q i, j i - полярный и азимутальный углы, образуемые векторами R и r i с осями координат. Приведённая форма разложения отличается от исходного ряда Тейлора только перегруппировкой слагаемых и введением сферич. ф-ций, поэтому совокупность 2 l + 1 независимых величин Q(l)m также наз. 2 l -польным моментом. Если все предыдущие моменты равны нулю, 2 l -польный момент не зависит от выбора начала системы координат.
Полученные соотношения позволяют дать более общее определение M. порядка l как системы зарядов, для к-рой мультипольный момент порядка l отличен от нуля, а все остальные мультипольные моменты равны нулю. Потенциал статич. поля M. порядка l убывает на бесконечности как R -(l +1). Такой характер спадания математически объясняется тем, что потенциал раскладывается в ряд по обратным степеням R, а физически связан с интерференцией полей от отд. зарядов, входящих в M. Кроме этого, M. обладает специфич. угл. зависимостью, определяемой l -й сферич. ф-цией. Характер убывания поля вдали от сложной системы зарядов позволяет заменить её совокупность M. соответствующего порядка (с соответствующими значениями мультиполь-ных моментов).
Вполне аналогично мультипольное разложение можно ввести для статич. магн. полей, создаваемых системой стационарных токов. Для этого необходимо провести разложение векторного потенциала магн. поля:
u i - скорость движения i -го заряда. В отличие от случая статич. электрич. полей, разложение потенциала статич. магн. поля начинается с дипольного вклада, т. к. магн. зарядов нет (магнитные монополи пока не обнаружены). Для первого члена разложения получим
где 
- магнитный момент системы.
След. члены разложения получаются аналогично. Общий член разложения векторного потенциала выражается через шаровые ф-ции.
Для непрерывных ограниченных распределений зарядов (источников и стоков) в приведённых выше ф-лах 
заменяется объёмным интегралом от соответствующей плотности заряда (тока).
Разложение по M. широко используется не только в задачах электро- и магнитостатики, но и в др. областях физики, напр. в акустике и общей теории относительности.
Инвариантность фазы электромагнитной волны. Законы преобразования частоты и волнового вектора электромагнитной волны. Эффект аберрации в астрономии.
Аберра́ция све́та (лат. aberratio, от ab от и errare блуждать, уклоняться) — изменение направления распространения света (излучения) при переходе из одной системы отсчёта к другой [1].
При астрономических наблюдениях аберрация света приводит к изменению положения звёзд на небесной сфере вследствие изменения направления скорости движения Земли. Различают годичную, суточную и вековую аберрации. Годичная аберрация связана с движением Земли вокруг Солнца. Суточная — обусловлена вращением Земли вокруг своей оси. Вековая аберрация учитывает эффект движения солнечной системы вокруг центра Галактики [2].
Явление аберрации света приводит также к неизотропности излучения движущегося источника. Если в системе покоя источника его излучение изотропно, то в системе отсчёта относительно которой он движется, это излучение будет неизотропным, с повышением интенсивности в направлении движения источника [1]
