Рассмотрим уравнения Максвелла в среде с диэлектрической проницаемостью  и магнитной проницаемостью
и магнитной проницаемостью 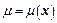 . Область за фронтом электромагнитного поля будет определяться неравенством
. Область за фронтом электромагнитного поля будет определяться неравенством  , где
, где 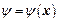 – функция координат. Собственное время фронта будет иметь вид
– функция координат. Собственное время фронта будет иметь вид  . Правую часть зададим в виде плотности тока
. Правую часть зададим в виде плотности тока 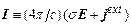 , где
, где 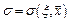 – проводимость среды, а
– проводимость среды, а 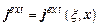 – плотность стороннего тока.
– плотность стороннего тока.
Напомним, как выводятся макроскопические уравнения Максвелла [6]. Рассмотрим микроскопические уравнения:
 (21)
(21)
Здесь  и
и  означают компоненты микроскопического электромагнитного поля, а
означают компоненты микроскопического электромагнитного поля, а  и
и  – микроскопические плотности заряда и тока, в том числе, ответственные за поляризацию и намагниченность среды.
– микроскопические плотности заряда и тока, в том числе, ответственные за поляризацию и намагниченность среды.
Рассмотрим ту пару уравнений Максвелла, которая не содержит  и
и  . Усредним их по пространственным переменным, обозначая
. Усредним их по пространственным переменным, обозначая 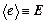 ,
, 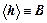 . Значок
. Значок 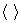 означает усреднение.
означает усреднение.
Пусть  , где
, где 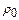 – плотность внешнего заряда, а
– плотность внешнего заряда, а 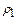 – плотность заряда, создающего поляризацию. На масштабах усреднения интеграл
– плотность заряда, создающего поляризацию. На масштабах усреднения интеграл  по любому объему равен нулю. Поэтому
по любому объему равен нулю. Поэтому  можно представить в виде
можно представить в виде 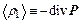 , где
, где 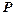 – векторное поле, которое называют поляризацией среды. Рассмотрим третье уравнение системы (21). Применяя к нему процедуру усреднения, получим уравнение
– векторное поле, которое называют поляризацией среды. Рассмотрим третье уравнение системы (21). Применяя к нему процедуру усреднения, получим уравнение
 (22)
(22)
где  – индукция электромагнитного поля.
– индукция электромагнитного поля.
Величина 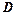 определена с точностью до любого соленоидального векторного поля. Продифференцируем (22) по времени и воспользуемся непрерывностью заряда:
определена с точностью до любого соленоидального векторного поля. Продифференцируем (22) по времени и воспользуемся непрерывностью заряда:
 (23)
(23)
Величина под знаком дивергенции в (23) может быть представлена в виде ротора некоторого векторного поля 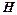 . Получим последнее макроскопическое уравнение Максвелла:
. Получим последнее макроскопическое уравнение Максвелла:
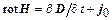 (24)
(24)
Для того, чтобы определить систему макроскопических уравнений Максвелла, постулируем, что 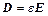 ,
,  .
.
Величины  и
и 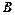 получены прямым усреднением компонент электромагнитного поля, которые являются компонентами тензора. Это означает, что
получены прямым усреднением компонент электромагнитного поля, которые являются компонентами тензора. Это означает, что
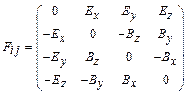 (25)
(25)
является кососимметричным тензором второго ранга типа  . Поскольку
. Поскольку 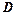 и
и 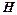 зависят от
зависят от  и
и 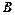 линейно, можно ввести тензор
линейно, можно ввести тензор
 , (26)
, (26)
который связан с тензором 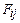 соотношением
соотношением 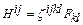 , где
, где 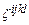 – кососимметричный по парам индексов
– кососимметричный по парам индексов 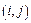 и
и  тензор, описывающий свойства среды.
тензор, описывающий свойства среды.
С помощью введенных тензоров уравнения Максвелла в среде могут быть записаны в следующем виде:
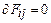 ,
, 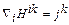 (27)
(27)
Уравнения (27) можно получить вариацией функционала действия, если действие для поля представить в виде  . Тогда тензор энергии-импульса можно записать в следующем симметричном виде:
. Тогда тензор энергии-импульса можно записать в следующем симметричном виде:
 .
.
Отсюда энергия в координатах  представляется в виде
представляется в виде 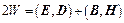 , а вектор Пойнтинга –
, а вектор Пойнтинга – 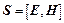 . В координатах
. В координатах 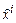
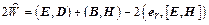 ,
, 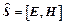 .
.
Уравнения (27) дают основание записывать уравнения Максвелла в среде в собственном времени  так:
так:
 ,
, 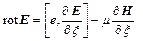 ,
,
где 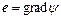 , энергию электромагнитного поля:
, энергию электромагнитного поля:
 ,
,
а закон ее сохранения
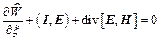 .
.
В системе координат 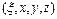 уравнения Максвелла имеют вид:
уравнения Максвелла имеют вид:
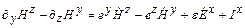 , (28)
, (28) 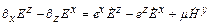 ,(32)
,(32)
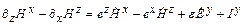 , (29)
, (29)  ,(32)
,(32)
 , (30)
, (30) 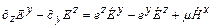 ,(33)
,(33)
где 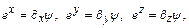
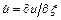 .
.
79. ……






