Применение

Непосредственно из определения следует, что

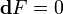
В компонентах это выражение принимает вид

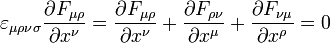
где 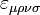— символ Леви-Чивиты для 4-хмерного пространства. Если расписать это выражение через компоненты векторов электрического и магнитного поля, то оно совпадёт с первой парой уравнений Максвелла:

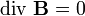
Вторая пара уравнений Максвелла выражается через тензор электромагнитного поля как

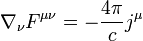
где 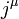— вектор 4-тока.

Также можно записать их через звёздочку Ходжа: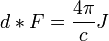

Сила Лоренца выражается через вектор 4-скорости частицы и заряд по формуле

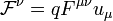
Преобразования Лоренца для полей
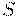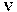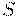Найдём связь электрического и магнитного полей, измеряемых наблюдателями в двух инерциальных системах отсчёта и . Обозначим через скорость системы относительно . Пусть сила, действующая на единичный заряд (), имеет лоренцевский вид:

где 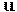— скорость частицы относительно 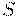. Любая сила в теории относительности преобразуется следующим образом (стр. \pageref{lorenz_force}):

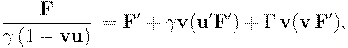
где, как обычно, и 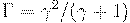. Если частица в 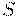покоится (), то её скорость в системе равна , поэтому:

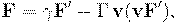
где учтено, что . При нулевой скорости 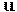в системе 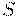сила равна электрическому полю , а в системе : :

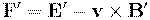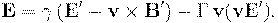
Поля не зависят от заряда и скорости пробной частицы, поэтому это преобразование выполняется при любых . Обратное преобразование, как обычно, получается при помощи замены :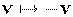

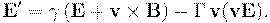
Это можно доказать, если сначала получить соотношение

следующее из (), а затем повторить предыдущие рассуждения, положив в () , и соответственно , .

Запишем теперь преобразование для силы () в случае, когда , и умножим его слева векторно на :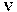

Подставим слева из (), а справа 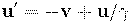[см. (), стр. \pageref{elect_vec_vec}, при ]. В результате, учитывая, что , получаем соотношение:

Таким образом, продольные (к скорости) компоненты электрического и магнитного полей одинаковы в обеих системах отсчёта.

Осталось найти преобразование для магнитного поля, аналогичное (). Для этого умножим () векторно на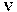

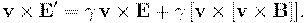
Подставляя справа из (), получаем:

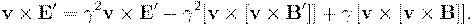
Раскроем двойное векторное произведение по формуле "бац минус цаб" и учтём, что :

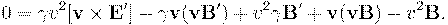
Учитывая, что , и перенося влево, окончательно получаем:

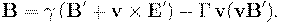
Обратное преобразование получается перестановкой штрихованных и нештрихованных величин и заменой .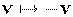

Таким образом, преобразования Лоренца для электрического и магнитного полей имеют следующий вид:

 

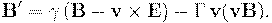
Их можно ( H) также расписать по компонентам:

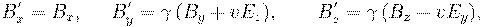
где ось 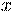выбрана в направлении относительной скорости: 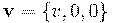. Заметим, что () формально можно получить из (), сделав замену: 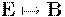и 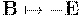. Кроме этого, полученные преобразования совпадают с преобразованиями компонент антисимметричного тензора второго ранга для момента импульса (стр. \pageref{moment_L_L_R}). Как мы увидим в следующей главе, это совпадение не случайно.

Аналогично упражнению 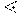H можно проверить инвариантность следующих скалярных выражений:

которые имеют одинаковое значение во всех инерциальных системах.

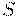Обратим внимание на тесную связь электрического и магнитного полей в преобразованиях () и (). Именно благодаря ей обычно говорят о едином электромагнитном поле, которое имеет два "лица": и . Они меняются при смене системы отсчёта, "порождая" друг друга. Например, пусть в системе нет магнитного поля . Тогда в системе будет наблюдаться магнитное поле, перпендикулярное как относительной скорости, так и электрическому полю. Действительно, из () и () следует:

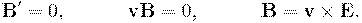
Получим ещё раз выражение для напряжённости электромагнитного поля движущегося со скоростью 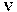заряда (стр.\pageref{E_B_main}). В системе отсчёта, в которой заряд покоится, магнитное поле равно нулю, а электрическое определяется законом Кулона:

Используя преобразования для электрического поля (), имеем:

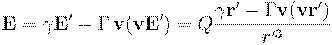
В момент времени , когда начала систем отсчёта совпадают, справедливы преобразования (), стр.\pageref{r3prime_electro}. Подставляя их, получаем:

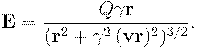
С учётом () магнитное поле равно 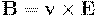, что совпадает с (), стр.\pageref{E_B_main}.

Заметим, что разделение на магнитное и электрическое поле единого силового влияния на пробную частицу достаточно условно. Магнитное поле содержится в составляющей силы, которая зависит от скорости частицы. Когда изменяется система отсчёта, меняется и скорость. Соответственно, происходит определённое перераспределение между электрическим и магнитным полями.

Можно было бы, конечно, работать с единым силовым полем 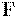. Однако в этом случае дифференциальные уравнения для такого поля оказались зависящими от скорости конкретной пробной частицы. Именно разделение силы 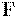на два поля позволило записать для них уравнения Максвелла, не зависящие от параметров пробной частицы. Это позволяет, решая уравнения, получать электрическое и магнитное поля, а затем выяснять, как они действуют (при помощи силы Лоренца) на любую пробную частицу или систему таких частиц.