Длина волны – расстояние между двумя ближайшими точками среды, в которых разность фаз колебаний равна 
.
Волновое число – число, которое показывает какое количество длин волн укладывается в отрезок .
Волновой вектор – вектор, по модулю равный волновому числу, и направленный вдоль луча в рассматриваемой точке среды.
Волна, типа 
, где 
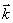- волновой вектор, называется плоской (можно писать в скалярной форме, т.к. все одинаково для магнитных и электрических полей).
Опр.: Если существует электромагнитная волна, в которой плоскость является геометрическим местом точек постоянной фазы, то волна плоская, а плоскость – фазовая.
- уравнение плоской бегущей электромагнитной волны (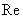
- действительная часть).
Поскольку 
, то волновое число 
(волновой вектор перпендикулярен фазовой плоскости). Другими словами для плоской волны первое уравнение Максвелла примет вид:
1) 
(т.к. 
- пустое пространство).
, 
, 
(для данного случая)
Т.е. для плоской волны первое уравнение Максвелла примет вид: 
2) 
Следовательно, второе уравнение Максвелла примет вид: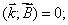 
3) 
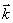
Другими словами, третье уравнение Максвелла для плоской волны примет вид: 
Поскольку: и 
то:
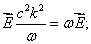
получили дисперсионное соотношение для плоской волны: 
. Другими словами: 
.
Ток и 4-потенциал, преобразование их компонент при изменении системы отсчета. Получение лоренцевских преобразований электрического и магнитного полей через преобразование потенциалов при изменении системы отсчета.
4-ток, четырёхток в специальной и общей теории относительности — лоренц-ковариантный четырёхвектор, который объединяет плотность тока электрических зарядов (или 3-вектор плотности тока любых других частиц) и объёмную плотность заряда (или объёмную концентрацию частиц).
где
— скорость света,
— скалярная плотность заряда,
— 3-вектор плотности тока,
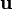— 3-вектор скорости зарядов.
В специальной теории относительности локальное сохранение электрического заряда выражается уравнением непрерывности, которое означает равенство нулю инвариантной дивергенции 4-тока:
где 
— 4-векторный оператор, называемый 4-градиентом и определяемый как 
. Здесь использовано соглашение Эйнштейна о суммировании по повторяющимся индексам. Вышеприведённое уравнение можно короче записать как
с обычным обозначением частной производной по данной координате как запятой перед соответствующим индексом.
В общей теории относительности уравнение непрерывности записывается так:
где точка с запятой перед индексом означает ковариантную производную по соответствующей координате.
В современной физике электромагни́тный потенциа́л обычно означает четырехмерный потенциал электромагнитного поля, являющийся 4-вектором (1-формой). Именно в связи с векторным (4-векторным) характером электромагнитного потенциала электромагнитное поле относится к классу векторных полей в том смысле, который употребляется в современной физике по отношению к фундаментальным бозонным полям (например, гравитационное поле является в этом смысле не векторным, а тензорным полем).
Обозначается электромагнитный потенциал чаще всего 
или 
, что подразумевает величину с индексом, имеющую четыре компоненты 
или 
, причём индексом 0 как правило обозначается временная компонента, а индексами 1, 2, 3 — три пространственных. В этой статье мы будем придерживаться первого обозначения.
В современной литературе могут использоваться более абстрактные обозначения.
В любой определенной инерциальной системе отсчета электромагнитный потенциал 
распадается[1] на скалярный (в трехмерном пространстве) потенциал 
и трехмерный векторный потенциал 
; эти потенциалы 
и 
- и есть те скалярный и векторный потенциалы, которые используются в традиционной трехмерной формулировке электродинамики. В случае, когда электромагнитное поле не зависит от времени (или быстротой его изменения в конкретной задаче можно пренебречь), то есть в случае (приближении) электростатики и магнитостатики, напряженность электрического поля выражается через ф, называемый в этом случае электростатическим потенциалом, а напряженность магнитного поля (магнитная индукция)[2] — только через векторный потенциал. Однако в общем случае (когда поля меняются со временем) в выражение для электрического поля входит также и векторный потенциал, тогда как магнитное — всегда выражается лишь через векторный (нулевая компонента электромагнитного потенциала в это выражение не входит).
Связь напряжённостей с электромагнитным потенциалом в общем случае такова в традиционных трехмерных векторных обозначениях[3]:
где 
— напряженность электрического поля, 
— магнитная индукция (или — что в случае вакуума в сущности то же самое — напряженность магнитного поля), 
— оператор набла, причём 
— градиент скалярного потенциала, а 
— ротор векторного потенциала.
В несколько более современной четырехмерной формулировке эти же соотношения можно записать как выражение тензора электромагнитного поля через 4-вектор электромагнитного потенциала:
где 
— тензор электромагнитного поля, компоненты которого представляют собой компоненты 
.
Приведенное выражение является обобщением выражения ротора для случая четырехмерного векторного поля.
При переходе от одной инерциальной системы отсчета к другой, компоненты преобразуются, как это свойственно компонентам 4-вектора, посредством преобразований Лоренца.
Физический смысл
Физический смысл четырехмерного электромагнитного потенциала можно прояснить, заметив, что этот потенциал при взаимодействии с заряженной частицей[4] (с электрическим зарядом q) дает добавку в фазу 
ее квантовой волны вероятности:
,
или, иначе говоря, вклад в действие (формула отличается от записанной выше только отсутствием множителя 
, а в системе единиц, где 
— просто совпадает с ней).
Физический смысл электрического и магнитного потенциалов в более простом частном случае электростатики и магнитостатики, а также единицы измерения этих потенциалов обсуждаются в статьях Электростатический потенциал и Векторный потенциал электромагнитного поля.
