Напомним, что если в электромагнитной волне вектор 
имеет единственное направление (а, следовательно, единственное направление имеет и вектор 
), то волна называется линейно-поляризованной. Ниже будут приведены доказательства того, что свет представляет собой электромагнитные волны, частоты которых лежат в определенном интервале. Если в световой волне вектор 
(и 
) имеет всевозможные направления, то такой свет принято называть естественным. Следовательно, свет как плоская электромагнитная волна может быть в однородной среде как естественным, так и линейно-поляризованным.
Электромагнитная волна может переносить электромагнитную энергию (поток энергии). Вычислим поток электромагнитной энергии в вакууме, исходя из уравнений Максвелла. Для этого умножим обе стороны уравнения (12.1) скалярно на , а обе стороны уравнения (12.2) – на 
:
, (12.18)
. (12.19)
Используем формулу векторного анализа
и, соответственно, вычтем из уравнения (12.18) выражение (12.19):
. (12.20)
Выражение (12.20) представляет собой запись закона сохранения энергии электромагнитного поля в дифференциальной форме. Рассмотрим физический смысл отдельных величин, входящих в уравнение (12.20). Частная производная 
представляет собой приращение электромагнитной энергии единицы объема за единицу времени, a 
– поток энергии, вытекающей из единицы объема за единицу времени. Вектор 
представляет собой поток энергии через единичную площадку, расположенную перпендикулярно потоку. При 
и 
поток постоянен и вектор 
выражает поток энергии за единицу времени, при переменных 
и он выражает мгновенное значение потока.
Введем обозначение:
, (12.21)
где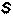 
называют вектором Умова–Пойнтинга. Этот вектор определяет направление распространения энергии волны.
Вычислим вектор Умова–Пойнтинга плоской электромагнитной волны:
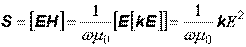. (12.22)
Согласно выражению (12.22), векторы S и k коллинеарны. Это справедливо только для вакуума и изотропных сред. В анизотропных средах, в которых физические свойства различны для разных направлений, это условие в общем случае не выполняется. Используем ранее введенный единичный вектор m, направленный вдоль распространения волны 
.
Поскольку для вакуума 
то
. (12.23)
Найдем соотношение между абсолютными значениями векторов 
и в плоской волне. Из уравнений (12.15) и (12.16) имеем:
. (12.24)
Имея в виду, что 
, получим:
. (12.25)
Учитывая, что векторы 
, , 
взаимно перпендикулярны, находим соотношение между абсолютными значениями векторов 
и :
. (12.26)
Из общего определения плотности электромагнитной энергии в вакууме
. (12.27)
С учетом уравнения (12.11) для плоской волны получим
. (12.28)
Запишем теперь окончательное выражение для вектора Умова–Пойнтинга в плоской волне:
. (12.29)
Полученное равенство имеет простой смысл. Через единичную площадку, поставленную перпендикулярно распространению волны, в единицу времени проходит энергия, заключенная в цилиндре с площадью основания, равной единице, и высотой 
.
63………
64.Преобразования Лоренца для четырехмерных (релятивистских) векторов – координат пространства-времени, плотностей токов и зарядов, энергии и импульса. Их простейшие инварианты.
Системы координат. Преобразования Лоренца
Для описания процессов соударения частиц а и b с образованием частиц
ci а + b → а' + b' + c1 + c2 +...+ cn наиболее часто применяются четыре системы координат:
лабораторная или L-система (ЛАБ);
симметричная или S-система (СИМ):
система центра масс или С-система (СЦМ);
зеркальная или М-система (ЗЕРК).
В лабораторной системе мишень покоится, т.е. рb = 0, Еb = mbc2, а 4-импульсы взаимодействующих частиц будут 
a{pa,Ea/c} и b{0, mbс}.
В симметричной системе сумма импульсов вторичных заряженных частиц равна нулю: ∑зарpi = 0.
Система центра масс – это система, в которой сумма импульсов сталкивающихся частиц равна нулю: pа* + Рb* = 0 (параметры частиц в этой системе будем обозначать знаком *).
Так. эксперименты на встречных пучках (ISR, ЦЕРН) проводятся в системе, близкой к СЦМ (пучки пересекаются под малым углом 15°).
В зеркальной (или антилабораторной) системе покоится налетающая частица, т.е. ра = 0, Еа = mас2. а 4-импульсы сталкивающихся частиц есть a{0,mac} и b{рb, Еb/с}.
Из приведенных выше определений систем отсчета видно их отношение к состоянию движения первичных частиц: в L-системе практически вся полная энергия системы сосредоточена до столкновения на частице а, в М-системе – на частице b, в С-системе сталкивающиеся частицы равноправны, эта система наиболее часто употребляется для описания процесса соударения.
Измерения обычно ведутся в лабораторной системе, а для анализа эксперимента используются другие системы.
Переход из одной системы координат в другую осуществляется с помощью преобразований Лоренца. В физике высоких энергий и физике космических лучей экспериментатор имеет дело со скоростями частиц, близкими к скорости света. Поэтому при переходе от одной системы отсчета к другой нужно пользоваться релятивистскими формулами преобразования в четырехмерном пространстве.
Как известно, релятивистская механика формулируется в четырехмерном пространстве, где сохраняется длина четырехмерного вектора. Другими словами, длина четырехмерного вектора с координатами x,y,z,ct является лоренц-инвариантом. Преобразования Лоренца устанавливают связь между координатами 4-вектора в лабораторной системе (x,y,z,ct) с его координатами в движущейся системе, например С-системе (x*, у*, z*, ct*).
Переход из С-системы в L-систему осуществляется с помощью матрицы
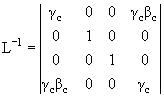
Если А – 4-вектор с координатами {x1x2x3x4} в L-системе, то А = L-1A*. где A*{x1*x2*x3*x4*} – 4-вектор в С-системе.
Аналогичен переход из L-систeмы в С-систeму: А* = L·A,
где 
– матрица перехода.
Пусть С-система движется так, что ее скорость vнаправлена вдоль оси х* и совпадает с направлением оси х лабораторной системы. При этом связь координат в L- и С-системах выразится соотношениями
х = γс(x* + vt), y = y*, z = z*, 
,
где
Для перевода 4-импульса *(рx*рy*рz*Е*) из С-системы в L-систему
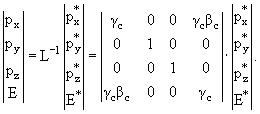
После применения матрицы L-1получаем для отдельных компонент 4-импульса следующие соотношения: рх = γс(рx* + βcE*), ру = py*, рz =рz*.
Е = γс(Е* + βcpх*).
Для перевода 4-импульса (pxpypzE) из L-системы в С-систему применяется матрица L
После этого получим для отдельных компонент 4-импульса: рх* = γс(рх – βcЕ), ру* = ру, pz* = pz,
Е* = γс(Е – βcpх).
4.2. Инварианты лоренцевских преобразований
1. 4-импульс {р, E}, квадрат 4-импульса 2 = Е2 – р2 = m2 является инвариантом
Все квадратичные формы 4-импульсов также являются инвариантами.
2. Инвариант квадрат эффективной массы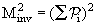 
, для двух частиц:
; 
,
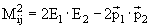если массами mi, и mj можно пренебречь.
3. Недостающая масса 
к частице с может быть вычислена по формулам
; 
4. Поперечный импульс 
является инвариантной величиной. Поперечная масса 
используется для определения энергии Еi, и продольного импульса
: 
, 
, где уi, – быстрота.
5. Быстрота 
.
При р ≈ Е псевдобыстрота 
Для этих величин инвариантами являются интервалы Δу и Δη.
Распределение dσ/dy – инвариант с точностью до переноса системы координат:
dσ/dy y = yс + y*;
ch y = (ey + e-y)/2;
sh y = (ey – e-y)/2.
Определение границ изменения быстроты частицы "с" в пределах от ymin до ymах дастся соотношениями:
6. Переменные Мандельштама s, t, u являются инвариантами:
s= ( а+ b)2; t = ( a – c)2; u = ( b – с)2.
7. Инвариантом лоренцевских преобразований является фазовый объем – область фазового пространства, разрешенная законами сохранения. Элемент фазового объема определяется через произведение дифференциалов 4-импульсов частиц.
С учетом законов сохранения элемент трехмерного инвариантного фазового объема можнize:
где δ-функция учитывает закон сохранения 4-импульса.
Полный фазовый объем – это интеграл по всем импульсам частиц конечного состояния
Ф(s) = ∫dФi.
простейшие инварианты.
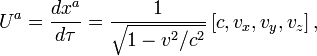
где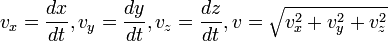 
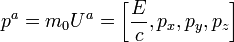
65.Преобразования Лоренца для электромагнитных полей (в векторном виде). Тензор электромагнитного поля, дуальный тензор и их инварианты.
Явный вид преобразований псевдоевклидовой плоскости
Лоренцевы преобразования псевдоевклидовой плоскости можно записать в наиболее простом виде, используя базис 
, состоящий из двух изотропных векторов:
Именно, в зависимости от знака определителя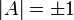 
, матрица преобразования в данном базисе имеет вид:
Знак числа 
определяет то, оставляет ли преобразование 
части светового конуса на месте 
, или меняет их местами 
.
Другой часто встречающийся вид матриц лоренцевых преобразований псевдоевклидовой плоскости получается при выборе базиса, состоящего из векторов 
и 
:
В базисе 
матрица преобразования имеет одну из четырёх форм:
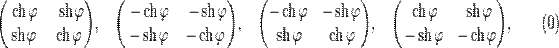
где 
и 
— гиперболические синус и косинус.
[править] Явный вид преобразований пространства сигнатуры (n-1,1)
Лоренцевы преобразования 
-мерного псевдоевклидова пространства 
со скалярным произведением
описываются следующей теоремой.
Вид преобразований при произвольной ориентации осей
В силу произвольности введения осей координат, многие задачи можно свести к указанному случаю. Если же задача требует иного расположения осей, то можно воспользоваться формулами преобразований в более общем случае. Для этого радиус-вектор точки
,
где 
— орты, надо разбить на составляющую 
параллельную скорости и составляющую 
ей перпендикулярную
.
Тогда преобразования получат вид
,
где 
— абсолютная величина скорости,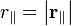 
— абсолютная величина продольной составляющей радиус-вектора.
Эти формулы для случая параллельных осей, но с произвольно направленной скоростью, можно преобразовать к виду, впервые полученному Герглоцем:
.
Обратите внимание, что самый общий случай, когда начала координат не совпадают в нулевой момент времени, здесь не приведён с целью экономии места. Его можно получить, добавив к преобразованиям Лоренца трансляцию (смещение начала координат).
Тензор электромагнитного поля, дуальный тензор и их инварианты.
Определение
Тензор электромагнитного поля определяется через 4-потенциал по формуле
Хотя он выражается через обычные производные, а не ковариантные, он является тензором относительно произвольных преобразований координат. Это следует из того, что то же выражение можно записать через ковариантные производные:
Если рассматривать 4-потенциал как 1-форму на пространстве-времени, то тензор электромагнитного поля выражается как внешняя производная
Отсюда также очевидна его инвариантность.
66………
