√радиент деп Ц бер≥лген потенциалдың басқа нүктемен салыстырғандағысына айтылады. —онда элкетростатикалық өр≥ст≥ң потенциалы нүктеден нүктеге өзгерет≥н функци€ болып табылады.

ћұндағы минус таңба q1 нүктел≥к зар€дты q зар€дын қашықтатып көш≥р≥лген нүктедег≥ потенциалдың б≥рте Цб≥рте кем≥п баруын көрсетед≥. —онда ≈ Ц кернеул≥к кер≥ таңбамен алынған потенциалдың градиент≥не тең болады. ернеул≥к бет бойынша ќстроградский-√аусс теоремасы бойынша таралады. ћұнда кез Ц келген тұйық беттен өтет≥н электрл≥к ығысу ағынының сол бетт≥ң ≥ш≥ндег≥ электр зар€дының арасындағы байланысты көрсетет≥н теорема. —онда, 
Өр≥ст≥ң бер≥лген нүктес≥ндег≥ өр≥с потенциалы деп аталатын

скал€рлық шама,  кернеул≥к векторымен қоса, электр өр≥с≥н сипаттау үш≥н пайдаланылады. —онда
кернеул≥к векторымен қоса, электр өр≥с≥н сипаттау үш≥н пайдаланылады. —онда 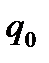 зар€дты 1-ш≥ нүктеден 2-ш≥ге орын ауыстырғандағы электростатикалық өр≥с күштер≥н≥ң атқаратын жұмысын мына түрде жазуға болады
зар€дты 1-ш≥ нүктеден 2-ш≥ге орын ауыстырғандағы электростатикалық өр≥с күштер≥н≥ң атқаратын жұмысын мына түрде жазуға болады
 .
. 
Ёлектростатикалық өр≥ст≥ң 1 және 2 нүктелер≥н≥ң потенциалдар айырмасы б≥рл≥к оң зар€дты 1-ш≥ нүктеден 2-ш≥ге орын ауыстырғандағы өр≥с күштер≥н≥ң атқаратын жұмысына тең:
 .
.
ѕотенциалдың өлшем б≥рл≥г≥ Ц вольт (¬): 1 л зар€дтың 1ƒж потенциалдық энерги€ны иеленет≥н өр≥с нүктес≥н≥ң потенциалы 1¬-қа тең деп алынады.
«ар€дтар жүйес≥н≥ң өр≥с потенциалы әр жеке зар€дтың туғызатын өр≥с потенциалдарының алгебралық қосындысына тең:
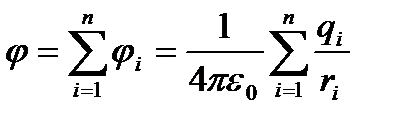 .
.
Ёлектростатикалық өр≥ст≥ң кернеул≥к векторының кез келген тұйық контур бойымен алынған циркул€ци€сы нөлге тең.
Ёлектростатикалық өр≥с кернеул≥г≥ мен потенциал арасындағы байланыс мына теңдеумен өрнектелед≥:
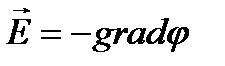 немесе
немесе  .
.
Ѕарлық нүктелер≥ндег≥ потенциалдың мәндер≥ б≥рдей беттерд≥ эквипотенциалды беттер деп атайды.
Ёквипатенциал беттерд≥ң қасиеттер≥:
1. ≈гер нүктел≥к зар€д эквипатенциал бетт≥ң бойымен орын ауыстырса оның ≥стеген жұмысы нолге тең болады. 
2. Өр≥с кернеул≥г≥н≥ң күш сызықтары әр уақытта эквипатенциал бетке нормаль болады. ≈гер ондай болмаса онда элкетр өр≥с≥ кернеул≥г≥ тангенциал немесе жанама болып атқарған жұмысы нолден өзгеше болады.
3. Ёлектростатикалық өр≥стег≥ электр өтк≥зг≥ш≥н≥ң бет≥ әр уақытта эквипатенциал беттер болады. —ебеб≥: егер зар€дтар цилиндр немесе шар
сфера тәр≥зд≥ өтк≥зг≥шт≥ң ос≥нде орналасса олардың электр өр≥с≥ күш сызықтары өтк≥зг≥шт≥ң бет≥не радиалды бағытталған болады.
|
|
|
4. Өр≥ст≥ң күш сызықтары өр≥с нүктес≥ндег≥ потенциалдық жылдамырақ өзгеру бағытын көрсетед≥. —онымен б≥ртект≥ өр≥с үш≥н эквипатенциал беттер
б≥р Цб≥р≥мен б≥рдей қашықтықта орналасқан өр≥ст≥ң бағытына перпендикул€р сызықтар жүйес≥ болып табылады.
ернеул≥к сызықтар эквипотенциалды беттерге үнем≥ нормаль бағытталады.
Өр≥с кернеул≥г≥ мен потенциалдың арасындағы байланысты белг≥л≥ өр≥с кернеул≥г≥ арқылы өр≥ст≥ң кез келген ек≥ нүктес≥н≥ң потенциалдар айырмасын анықтау үш≥н пайдалануға болады.
ернеул≥к сызықтары деп әр нүктес≥нде жүрг≥з≥лген жанамалары өр≥ст≥ң сол нүктес≥ндег≥  кернеул≥к векторымен бағыттас болатындай ет≥п жүрг≥з≥лген сызықтарды атайды. ернеул≥к сызықтарын оларға перпендикул€р орналасқан б≥рл≥к бет арқылы өтет≥н сызықтар саны сол жердег≥ өр≥с кернеул≥г≥н≥ң
кернеул≥к векторымен бағыттас болатындай ет≥п жүрг≥з≥лген сызықтарды атайды. ернеул≥к сызықтарын оларға перпендикул€р орналасқан б≥рл≥к бет арқылы өтет≥н сызықтар саны сол жердег≥ өр≥с кернеул≥г≥н≥ң 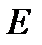 модул≥не тең (немесе пропорционал) болатындай қоюлықпен жүрг≥зед≥. Ёлектростатикалық өр≥ст≥ң кернеул≥к сызықтары зарадтан басталып шекс≥зд≥кке кетед≥ (оң зар€д үш≥н), немесе, шекс≥зд≥ктен кел≥п зар€дта а€қталады (тер≥с зар€д үш≥н).
модул≥не тең (немесе пропорционал) болатындай қоюлықпен жүрг≥зед≥. Ёлектростатикалық өр≥ст≥ң кернеул≥к сызықтары зарадтан басталып шекс≥зд≥кке кетед≥ (оң зар€д үш≥н), немесе, шекс≥зд≥ктен кел≥п зар€дта а€қталады (тер≥с зар€д үш≥н).
≈гер өр≥ст≥ң кез келген нүктес≥нде кернеул≥к векторының модул≥ және бағыты б≥рдей болса  , ондай өр≥с б≥ртект≥ деп аталады. Ѕ≥ртект≥ өр≥ст≥ң кернеул≥к сызықтары б≥ркелк≥ қоюлықпен жүрг≥з≥лген өзара параллель сызықтар болып табылады.
, ондай өр≥с б≥ртект≥ деп аталады. Ѕ≥ртект≥ өр≥ст≥ң кернеул≥к сызықтары б≥ркелк≥ қоюлықпен жүрг≥з≥лген өзара параллель сызықтар болып табылады.
ернеул≥к векторының тұйқталған бет арқылы ағынын √аусс теоремасы анықтайды:

ернеул≥к векторының ағыны деп Ц белг≥л≥ б≥р бетт≥ тес≥п өтет≥н кернеул≥к сызықтарының жалпы санына айтылады. јғынды ‘ - әр≥п≥мен бел≥г≥лейм≥з. 
≈герде кернеул≥к бетке бұрыш астында түсет≥н болса онда cos  қосылады.
қосылады.
 . јл егерде кернеул≥к б≥р тект≥ болмаса онда кернеул≥к ағыны бетт≥к интегралдау жолымен табылады.
. јл егерде кернеул≥к б≥р тект≥ болмаса онда кернеул≥к ағыны бетт≥к интегралдау жолымен табылады. 
≈герде аудан мен кернеул≥к б≥р-б≥р≥не параллель болса онда кернеул≥к векторы нөлге айналады. —ебеб≥: ф=0 

Ѕұдан мынадай тұжырым шығады. ≈гер кернеул≥к сызықтары нормальмен сүй≥р бұрыш жасаса  онда кернеул≥кт≥ң векторының ағыны үлкен нөл немесе оң болады. јл
онда кернеул≥кт≥ң векторының ағыны үлкен нөл немесе оң болады. јл  болса онда вектордың ағыны к≥ш≥ ноль немесе тер≥с таңбалы болады. «ар€дтың сызықтық тығыздығы деп денен≥ң б≥рл≥к ұзындығына келет≥н зар€дты атайды:
болса онда вектордың ағыны к≥ш≥ ноль немесе тер≥с таңбалы болады. «ар€дтың сызықтық тығыздығы деп денен≥ң б≥рл≥к ұзындығына келет≥н зар€дты атайды:
 , л/м.
, л/м.
«ар€дтың бетт≥к тығыздығы деп аудан б≥рл≥г≥не келет≥н зар€дты атайды:
 , л/м2.
, л/м2.
«ар€дтың көлемд≥к тығыздығы деп денен≥ң б≥рл≥к көлем≥не келет≥н зар€дты атайды:
 , л/м3
, л/м3
¬акуумдег≥ электростатикалық өр≥с үш≥н √аусс теоремасы: кез келген тұйық бет арқылы өтет≥н вакуумдег≥ электростатикалық өр≥ст≥ң кернеул≥к векторының ағыны сол бетпен қоршалған зар€дтардың алгебралық қосындысының  -ге қатынасына тең:
-ге қатынасына тең:
|
|
|
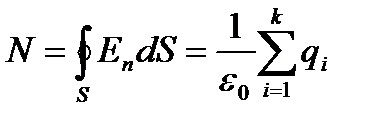 .
.
1. Ѕ≥ртект≥ зар€дталған шекс≥з ж≥пт≥ң өр≥с≥
 ,
,
мұндағы  - ж≥п пен қарастырылып отырған нүктен≥ң ара қашықтығы.
- ж≥п пен қарастырылып отырған нүктен≥ң ара қашықтығы.
2. Ѕ≥ртект≥ зар€дталған шекс≥з жазықтықтың өр≥с≥
 .
.
3. ≈к≥ әр аттас зар€дталған өзара параллель шекс≥з жазықтықтардың өр≥с≥
 .
.
4. Ѕ≥ртект≥ зар€дталған сфералық бетт≥ң өр≥с≥

 үш≥н,
үш≥н,

 үш≥н,
үш≥н,
мұндағы  - сфера центр≥нен өр≥ст≥ң қарастырылып отырған нүктес≥не дей≥нг≥ ара қашықтық.
- сфера центр≥нен өр≥ст≥ң қарастырылып отырған нүктес≥не дей≥нг≥ ара қашықтық.
5. өлем бойынша зар€дталған шардың өр≥с≥

 үш≥н,
үш≥н,

 үш≥н,
үш≥н,
мұндағы  - сфера центр≥нен өр≥ст≥ң қарастырылып отырған нүктес≥не дей≥нг≥ арақашықтық.
- сфера центр≥нен өр≥ст≥ң қарастырылып отырған нүктес≥не дей≥нг≥ арақашықтық.
√аусс теоремасы симмери€лы электр өр≥стер≥н есептеу үш≥н кең қолданылады. Ѕұл теореманы қолданып б≥ркелк≥ зар€дталған шекс≥з жазықтың, сфераның, цилиндрд≥ң өр≥сн оп-оңай есептеп шығуға болады. √аус теоремасының дифференциалдық түр≥ кең≥ст≥кт≥ң белг≥л≥ б≥р нүктес≥ндег≥ өр≥с кернеул≥г≥н сол нүктедег≥ зар€д тығыздығымен байланыстырады:

Ёлектрл≥к ығысу векторы деп Ц сан жағынан электр кернеул≥к вектордың абсалютт≥к диэлектрл≥к өт≥мд≥л≥к пен көбейт≥нд≥с≥не тең шамаға айтылады. јл абсалютт≥к диэлектрикт≥к өт≥мд≥л≥к деп вакумдағы диэлектрл≥к өт≥мд≥л≥кпен ортадағы диэлектрл≥к өт≥мд≥л≥кт≥ң көбейт≥нд≥с≥не айтылады. ќны ƒ әр≥п≥мен белг≥лейм≥з.
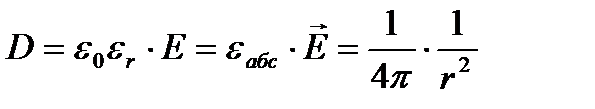
 .
.
ƒ Ц шама ортаның қасиет≥не тәуелс≥з.
≈гер электрл≥к ығысу әртүрл≥ болса тағыда интегралдау жолымен табылады.

Ёлектр дипол≥ деп б≥р≥нен-б≥р≥  ара қашықтыққа ығысқан ек≥ шамалары б≥рдей
ара қашықтыққа ығысқан ек≥ шамалары б≥рдей  және -
және -  әр аттас нүктел≥к зар€дтан тұратын жүйен≥ атайды. ≈гер
әр аттас нүктел≥к зар€дтан тұратын жүйен≥ атайды. ≈гер  ара қашықтығы жүйе өр≥с≥н≥ң нүктелер≥не дей≥нг≥ ара қашықтықпен салыстырғанда әлде-қайда к≥ш≥ болса дипольд≥ элементар дейд≥.
ара қашықтығы жүйе өр≥с≥н≥ң нүктелер≥не дей≥нг≥ ара қашықтықпен салыстырғанда әлде-қайда к≥ш≥ болса дипольд≥ элементар дейд≥.
“ер≥с зар€дтан оң зар€дқа жүрг≥з≥лген  векторы диполь и≥н≥ деп аталады.
векторы диполь и≥н≥ деп аталады.
ƒипольд≥ң электрл≥к момент≥:
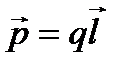 .
.
ƒиполь өр≥с≥ оның электрл≥к момент≥мен анықталады:
 ,
,
мұндағы  Ц дипольд≥ң
Ц дипольд≥ң  момент≥н≥ң бағыты мен дипольден өр≥ст≥ң қарастырылып отырған нүктес≥не жүрг≥з≥лген
момент≥н≥ң бағыты мен дипольден өр≥ст≥ң қарастырылып отырған нүктес≥не жүрг≥з≥лген  радиус-векторының бағыты арасындағы бұрыш.
радиус-векторының бағыты арасындағы бұрыш.
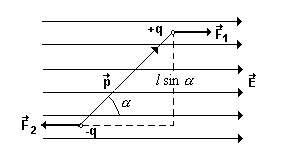
—ыртқы б≥ртект≥ электр өр≥с≥нде дипольге қос күш әсер етед≥. Қос күшт≥ң момент≥ мына өрнекпен анықталады
 .
.
Қос күш момент≥н≥ң модул≥ мынаған тең
 ,
,
мұндағы  Ц
Ц  векторы мен
векторы мен  өр≥с кернеул≥г≥н≥ң арасындағы бұрыш.
өр≥с кернеул≥г≥н≥ң арасындағы бұрыш.
Ѕұл қос күш  және
және  векторлары бағыттас болатындай ет≥п дипольд≥ бұруға тырысады. (7.1-сурет)
векторлары бағыттас болатындай ет≥п дипольд≥ бұруға тырысады. (7.1-сурет)
 7.1-сурет.
7.1-сурет.
≈гер диполь б≥ртект≥ емес өр≥сте орналасып, өр≥ске параллель жатпаса, онда дипольге оны өр≥ске параллель болатындай ет≥п бұруға тырысатын қос күшпен б≥рге дипольд≥ күшт≥рек өр≥с аймағына тартатын күш әсер етед≥.

1. ≈к≥ әр аттас зар€дталған өзара параллель шекс≥з жазықтықтың (жазық конденсатор) арасындағы потенциалдар айырмасы:
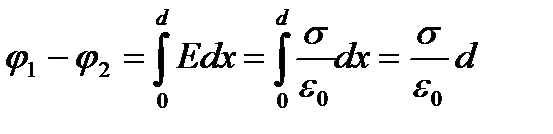 , мұндағы
, мұндағы  - жазықтықтардың ара қашықтығы.
- жазықтықтардың ара қашықтығы.
|
|
|
2. ≈к≥ зар€дталған коаксиалды цилиндрд≥ң (цилиндрл≥к конденсатор) арасындағы потенциалдар айырмасы: 
 , мұндағы
, мұндағы  және
және  Ц цилиндлерд≥ң радиустары.
Ц цилиндлерд≥ң радиустары.
3. ≈к≥ зар€дталған концентрл≥ сфераның арасындағы (сфералық конденсатор) потенциалдар айырмасы:

ќқшауланған өтк≥зг≥шт≥ң потенциалы оның зар€дына пропорционал:
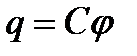 .
.
ѕотенциал мен зар€д арасындағы  пропорционалдық коэффициентт≥н өтк≥зг≥шт≥ң электр сыйымдылығы деп атайды. —ыйымдылық сан жағынан өтк≥зг≥шт≥ң потенциалын б≥р өлшемге арттыру үш≥н өтк≥зг≥шке бер≥лет≥н зар€дқа тең:
пропорционалдық коэффициентт≥н өтк≥зг≥шт≥ң электр сыйымдылығы деп атайды. —ыйымдылық сан жағынан өтк≥зг≥шт≥ң потенциалын б≥р өлшемге арттыру үш≥н өтк≥зг≥шке бер≥лет≥н зар€дқа тең:
 .
.
Ёлектр сыйымдылығының өлшем б≥рл≥г≥ - фарад (‘): 1 л зар€д бер≥лгенде потенциалын 1 ¬-қа өзгертет≥н оқшауланған өтк≥зг≥шт≥ң сыйымдылығы 1‘-қа тең деп алынады.
Өтк≥зг≥шт≥ң сыйымдылығы оның өлшемдер≥ мен п≥ш≥н≥не тәуелд≥. ћысалы, радиусы  шар тәр≥зд≥ өтк≥зг≥шт≥ң сыйымдылығы:
шар тәр≥зд≥ өтк≥зг≥шт≥ң сыйымдылығы:  .
.
Өлшемдер≥ шамалы және қоршаған денелермен салыстырғанда потенциалы азғантай болғанымен, өздер≥нде едәу≥р зар€дты жинақтай алатын құрылғыны конденсатор деп атайды. онденсатор б≥р≥нен-б≥р≥ диэлектрик қабатымен бөл≥нген қос өтк≥зг≥штен (астарлардан) тұрады. Өр≥с конденсатордың ≥ш≥нде ғана жинақталады, ал кернеул≥к сызықтары оның б≥р астарларынан басталып ек≥нш≥с≥нде а€қталады.
онденсатордың сыйымдылығын мына өрнект≥ң көмег≥мен анықтайды:
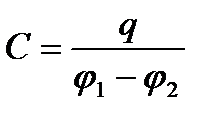 ,
,
мұндағы  Ц астарлардың б≥реу≥ндег≥ зар€д,
Ц астарлардың б≥реу≥ндег≥ зар€д,  - конденсатор астарларының арасындағы потенциалдар айырмасы.
- конденсатор астарларының арасындағы потенциалдар айырмасы.
¬акуумд≥ конденсатордың сыйымдылығы  , ал астарлары арасындағы кең≥ст≥к б≥ртект≥ диэлектрикпен толтырылған сол конденсатордың сыйымдылығы
, ал астарлары арасындағы кең≥ст≥к б≥ртект≥ диэлектрикпен толтырылған сол конденсатордың сыйымдылығы  болсын. —онда
болсын. —онда

қатынасын диэлектрикт≥ң салыстырмалы диэлектрл≥к өт≥мд≥л≥г≥ деп атайды.
1. ∆азық конденсатордың сыйымдылығы
 ,
,
ал диэлектрикпен толтырылған жазық конденсатордың сыйымдылығы
 .
.
2. ÷илиндрл≥к конденсатордың сыйымдылығы
 ,
,
ал диэлектрикпен толтырылған цилиндрл≥к конденсатордың сыйымдылығы
 .
.
3. —фералық конденсатордың сыйымдылығы
 ,
,
ал диэлектрикпен толтырылған сфералық конденсатордың сыйымдылығы
 .
.
Ѕер≥лген кернеу үш≥н керект≥ сыйымдылықты алу мақсатында конденсаторларды б≥р-б≥р≥мен батаре€ құрып жалғайды.
1. онденсаторларды параллель жалғау 
2. онденсаторларды т≥збектей жалғау  .
.
Өтк≥зг≥шт≥ң ≥шк≥ бөл≥ктер≥нде зар€дтың болмауы √аусс теоремасының салдары болып табылады. јл √аусс теоремасының өз≥ улон заңына нег≥зделген.
Ѕ≥р б≥р≥нен  ара қашықтықта орналасқан нүктел≥к
ара қашықтықта орналасқан нүктел≥к  және
және 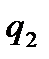 зар€дтардың өзара потенциалдық энерги€сын
зар€дтардың өзара потенциалдық энерги€сын 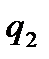 зар€дының өр≥с≥нде орналасқан
зар€дының өр≥с≥нде орналасқан  зар€дының потенциалдық энерги€сы, немесе
зар€дының потенциалдық энерги€сы, немесе  зар€дының өр≥с≥нде орналасқан
зар€дының өр≥с≥нде орналасқан 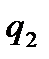 зар€дының потенциалдық энерги€сы деп қарастыруға болады:
зар€дының потенциалдық энерги€сы деп қарастыруға болады:
 ,
,
мұндағы  және
және 
-  зар€ды орналасқан нүктедег≥
зар€ды орналасқан нүктедег≥ 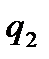 зар€ды тудыратын және
зар€ды тудыратын және 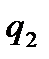 зар€ды орналасқан нүктедег≥
зар€ды орналасқан нүктедег≥  зар€ды тудыратын потенциалдарға сәйкес.
зар€ды тудыратын потенциалдарға сәйкес.
|
|
|
“ыныштық күйдег≥  зар€д үш≥н нүктел≥к зар€дтар жүйес≥н≥ң өзара әрекеттесу энерги€сы
зар€д үш≥н нүктел≥к зар€дтар жүйес≥н≥ң өзара әрекеттесу энерги€сы
 ,
,
мұндағы  Ц жүйен≥ң
Ц жүйен≥ң  -ш≥ зар€дынан басқа, барлық зар€дтарының
-ш≥ зар€дынан басқа, барлық зар€дтарының  зар€ды орналасқан нүктедег≥ тудыратын потенциалы:
зар€ды орналасқан нүктедег≥ тудыратын потенциалы:
 .
.
ќқшауланған өтк≥зг≥шт≥ң бет≥ эквипотенциалды болып табылады, €ғни  . Өтк≥зг≥ш бет≥ндег≥
. Өтк≥зг≥ш бет≥ндег≥  зар€дты
зар€дты  нүктел≥к зар€дтар жүйес≥ деп қарастыруға болады. —онда
нүктел≥к зар€дтар жүйес≥ деп қарастыруға болады. —онда
 .
.
Өтк≥зг≥ш бет≥ндег≥ зар€дпен оның потенциалының арасындағы байланысты ескере отырып, зар€дталған өтк≥зг≥шт≥ң энерги€сы үш≥н төмендег≥дей өрнектерд≥ жазуға болады:
 .
.
«ар€ды +  конденсатор астарының потенциалы
конденсатор астарының потенциалы  -ге, ал зар€ды -
-ге, ал зар€ды -  астарының потенциалы
астарының потенциалы  Цге тең болды дел≥к. —онда
Цге тең болды дел≥к. —онда
 .
.
онденсатор астарларындағы зар€д пен олардың арасындағы потенциал айырмасының байланысын ескере отыра зар€дталған конденсатор энерги€сы үш≥н мына өрнектерд≥ жазуға болады:
 .
.
онденсатор астарлары б≥р-б≥р≥н тартатын механикалық (пондеромоторлық) күшт≥ жазық конденсатордың потенциалдық энерги€сы арқылы анықтауға болады:
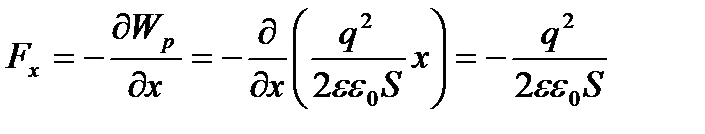 .
.
«ар€дталған конденсатордың энерги€сы оның электр өр≥с≥нде, €ғни оның астарларының арасындағы кең≥ст≥кте шоғырланған. онденсатордың энерги€сын оның электр өр≥с≥н сипаттайтын шамалар арқылы өрнектеуге болады. ∆азық конденсатор үш≥н мына өрнект≥ жазуға болады:
 ,
,
мұндағы  - өр≥ст≥ң алып отырған көлем≥.
- өр≥ст≥ң алып отырған көлем≥.
≈гер өр≥с б≥ртект≥ болса, онда оның ≥ш≥ндег≥ энерги€ кең≥ст≥кте  тұрақты тығыздықпен таралады:
тұрақты тығыздықпен таралады:
 .
.
Ёлектр тогы деп зар€дтардың реттелген қозғалысын айтамыз. Ёлектр тогын сандық сипаттау үш≥н ток күш≥ деген шама енг≥з≥лед≥. “ок күш≥ деп өтк≥зг≥шт≥ң көлденең қимасынан б≥рл≥к уақытта өтет≥н зар€дты айтады:
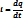
“ұрақты тогта 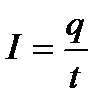
 1ј=
1ј= 
Ёлектр тогының пайда болудың ек≥ шарты бар:
1. зар€дтар денеде атомдармен байланысты болмаған ерк≥н электрондар.
2. —ол электрондарды бағытталған, қозғалысқа келт≥рет≥н электр өр≥с≥ болуы керек.
ќм өтк≥зг≥ш ұштарындағы кернеу мен онан өтет≥н ток күш≥н байланыстыратын заңдылықты ашты:
I= 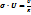
ћеталдарда пайда болған ток кернеуге пропорционал. 

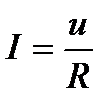 “≥збек бөл≥г≥ үш≥н ќм заңы.
“≥збек бөл≥г≥ үш≥н ќм заңы. 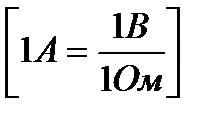
“ұрақты ток Ц деп уақыт өту≥мен шамасы және бағыты өзгермес болатын токтарға айтылады. “ұрақты токты акуммул€тор, голвани элементтер, батарейкалар беред≥ және олар тұрақты ток көздер≥ болып саналады.
Ёлектростатикалық күштерд≥ң тұйық контурдағы жұмысы нөлге тең, сондықтан тұрақты ток жүру үш≥н т≥збекте табиғаты кулондық емес күштер керек. Ѕұл күштерд≥ тосын (бөгде) күштер деп атайды. “осын күштерд≥ң б≥рл≥к зар€дқа әсер етет≥н күш≥н Ё.қ.к. (электр қозғаушы күшЦ ε) деп атайды. ≈гер т≥збек бөл≥г≥нде тосын күштер әсер етсе ќм заңын (т≥збект≥ң б≥р тект≥ емес бөл≥г≥ үш≥н) былай жазуға болады:

Ёлектр қозғаушы күш Ц деп ерк≥н зар€дтарды тасымалдау жұмысын жасайтын бөгде күштерге айтылады. ќны ток көздер≥ тудырады. ќны
 эпсилион мен белг≥лейм≥з.
эпсилион мен белг≥лейм≥з.
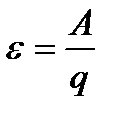


≈гер т≥збек тұйықталған болса ќм заңын төмендег≥ше жазуға болады:

“ок жүр≥п тұрған өтк≥зг≥ш ≥ш≥ндег≥ өр≥с кернеул≥г≥ мен ток тығыздығын байланыстыратын теңдед≥ ќм заңының дифференциалды түр≥ деп атайды:

“ок тығыздығы деп -т≥збектег≥ тогтың өтк≥зг≥ш көлденең қимасынан өт≥п тұратын зар€дтан концентраци€сымен жылдамдығының көбейт≥нд≥с≥не айтылады. Ќемесе жай т≥лмен айтқанда өт≥п жатқан ток күш≥н≥ң сол жердег≥ көлденең қимасын айтады.
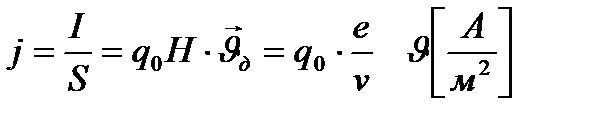
Өтк≥зг≥штег≥ электр күш теоремасы Ц дегенде өтк≥зг≥ш арқылы электрондардың қозғалысымен түс≥нд≥рет≥н теори€ға айтылады. ћұны б≥р≥нш≥ болып экспериментте 1913 ж совет физиктер≥ ћонделштам және ѕополекси 1916 ж јмерика физиктер≥ өз тәж≥рибелер≥нде дұрыс екенд≥г≥
|
|
|
дәлелдеген.
ќсы теорема бойынша жүзеге келет≥н электр өр≥с≥.
 мұны ƒжоуль Ц Ћенц тапқан.
мұны ƒжоуль Ц Ћенц тапқан.
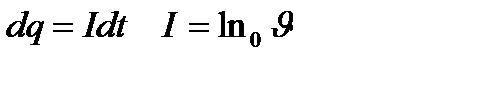
n Ц консентраци€ Ц көлем б≥рл≥г≥ндег≥ молекулалар саны.
атушкаға оралған сымның көлем≥ 
≈герде көлем бойынша қозғалыс мөлшер≥н өзгер≥с≥ мен өр≥с≥н≥ң өзгер≥с≥н өзара тең деп алып 
Өзара тең деп алсақ онда dq Цды табамыз 
“армақталған т≥збектер. ирхгоф ережелер≥. “ұрақты токтың жұмысы мен қуаты. ƒжоульЦЋенц заңы және оның дифференциалды түр≥.
“армақталған т≥збектерд≥ есептеу үш≥н ирхгоф тағайындаған ек≥ ережен≥ қолданады: б≥р≥нш≥ ереже, түй≥ндег≥ токтардың алгебралық қосындысы нөлге тең; ек≥нш≥ ереже, контурдағы кернеу құлауларының алгебралық қосындысы сол контурдағы э.қ.к. қосындысына тең


“ұрақты токтың жұмысы мен қуатын энерги€ның сақталу заңын қолданып алады. ƒжоуль мен Ћенц тәж≥рбе жүз≥нде ток жүр≥п тұрған өтк≥зг≥штен бөл≥нет≥н жылуды есптеп шығаратын заңдылықты тапты:
Q = I2Rt = IUt
“октың жұмысы деп - тогы бар т≥збектен уақыт бойынша өт≥п тұрған тог күш≥ өтк≥зг≥ш ұштарындағы кернеу және осы уақыттың шамаларының көбейт≥нд≥с≥не тең болған физикалық шамаға айтылады.
“≥збектеп қосылса ј=I2Rt A=IUt, параллель қосылса
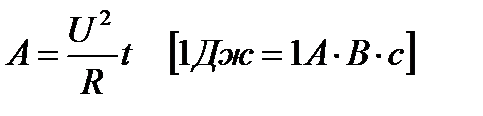
ƒжоуль- Ћенц заңы тогы бар өтк≥зг≥штен ажыралып шығатын жылулық мөлшер≥ сондағы токтың атқарған жұмысына тең болады.
 бұл табиғаттағы заттардың орын ауыстыруынан болатын жұмыс
бұл табиғаттағы заттардың орын ауыстыруынан болатын жұмыс  бұл деген≥м≥з тұрақты токтың атқарған жұмысы сол токтың өту уақыты мен анықталады.Өйткен≥ бұл жерде
бұл деген≥м≥з тұрақты токтың атқарған жұмысы сол токтың өту уақыты мен анықталады.Өйткен≥ бұл жерде
t- өзгер≥п тұрады.
ќм заңы 1 заңы т≥збект≥ң б≥р бөл≥г≥ үш≥н ќм заңы деп өтк≥зг≥штен өт≥п жатқан ток күш≥ оған қиылған кернеу тура пропорцианал, ал кедерг≥ге кер≥ пропорционал болады.

2- заңы. “олық т≥збек үш≥н ќм заңы деп Ц т≥збектен өт≥п жатқан ток күш≥ оған қосылған электр қозғаушы күш≥не тура т≥збек кедерг≥с≥мен ток көз≥ ≥шк≥ кедерг≥с≥н≥ң қосындысына кер≥ пропорционал болады.
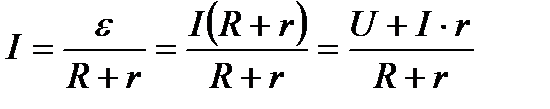
3. Ёлектр кедерг≥с≥ металдар үш≥н.
ћеталдық менш≥кт≥ кедерг≥с≥ мен ұзындығының көбейт≥нд≥с≥не тура пропорционал ал көлденең қимасының ауданына кер≥ пропорционал болады.

4. «аттың ≥шк≥ кедерг≥с≥.

өлденең қимасының ауданы 1 мм2-да бер≥лсе онда 10-6 жүред≥.
5. Ёлектр өтк≥зг≥шт≥к -деп заттың электр кедерг≥с≥не кер≥ болған физикалық шамаға айтылады. Өлшем б≥рл≥г≥: 
6. Өтк≥зг≥шт≥ң ¬ольт јмперл≥к сипаттамасы Ц деп әр түрл≥ өтк≥зг≥штердег≥ токтың кернеуге байланысқан тәуелд≥л≥г≥н айтады.

7. ћенш≥кт≥ электр өтк≥зг≥шт≥к Ц деп өтк≥зг≥шт≥ң менш≥кт≥ кедерг≥с≥не кер≥ болған физикалық шамаға айтылады. ќны j- мен белг≥лейм≥з.

8. ќм заңының дифференциалдық түр≥.







