1. Диэлектрик өтімділігі өте жоғары.
2. Диэлектриктер өрісі кернеулігімен индукция.
Векторлары өзара сызықты байланысқан.
3. Диэлектриктік өтімділік электр өрісі кернеулігіне тәуелді.
4. Поляризация уақытында дипольдық моменттердің электр өрісі кернеулігінің кешігіп жүруі.
Дипольдік моменттің электр өрісі кернеулігімен кемігу сызығына гистерезис деп аталады. Мұндай құбылыс магниттелетін заттарда ұшырайды яғнни кездеседі. Сонда қалдық магнетизмнің әсерінен бір түрлі заттар өзінің магниттелу қасиеттерін сақтап қалып тұрақты магнитке айналады. Бірақ оларда өздерінің кюри температурасына ие. Мұндай зерттеулер негізінен лабараториялық жұмыстармен дәлелденген. Ал табиғатта оны бұл құбылысты өте қиын. Себебі температурадан тыс ол заттарға өте күрделі күштер әсер етуінен және табиғаттағы перомагнетиктер жер қыртысында өте шұңқырда жатады.
1820 жылы дат физигі Х. Эрстед магнит тілшесіне электр тогының бағыттайтын әсерін байқаған. Сол аралықта француз физигі А.М. Ампер тогы бар екі өткізгіштің өзара әсерлесуін ашып, толығымен зерттеді. Магниттік өзара әсерлесу тек қозғалыстағы электр зарядтарына (токтарға) тән екендігі анықталды. Токтардың магниттік өзара әсерлесуі материяның ерекше түрі – магнит өрісі -арқылы жүзеге асады. Магнит өрісінің негізгі қасиеті – сол өрісте орналасқан тогы бар өткізгішке күштің әсер етуі. Магнит өрісінің қасиеттерін зерттеу үшін тогы бар рамка қолданылады.
Берілген нүктедегі магнит өрісінің бағыты ретінде рамкаға жүргізілген 
оң нормалінің өрістегі бағыты алынады. Тогы бар рамкаға әсер ететін күштер жұбының айналдыру моменті
,
мұндағы 
- тогы бар рамканың магниттік моменті, 
- магнит индукциясының векторы деп аталатын магнит өрісінің сандық сипаттамасы.
Біртекті магнит өрісінің берілген нүктесіндегі магнит индукциясы магниттік моменті бірге тең рамкаға, оған жүргізілген оң нормаль өріс бағытына перпендикуляр болғандағы, әсер ететін максималды айналдыру моменті арқылы анықталады.
Магнит индукцияның өлшем бірлігі - тесла (Тл).
элементі өрістің кейбір нүктесінде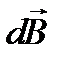 
индукциясын тудыратын 
тогы бар өткізгіш үшін Био-Савар-Лаплас заңы төмендегідей өрнектеледі.
,
мұндағы 
- токтың элементінен өрістің қарастырылып отырған нүктесіне жүргізілген радиус-векторы, 
= 4π·10-7 Гн/м – магнит тұрақтысы. 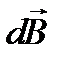- ның бағыты 
және векторларының бағытына перпендикуляр, яғни олар жатқан жазықтыққа перпендикуляр. Бұл бағытты оң бұрғы ережесі бойынша анықтауға болады: егер бұрғының ілгерілемелі қозғалысының бағыты элементтегі токтың бағытымен дәл келсе, онда бұрғы сабының айналу бағыты 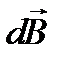векторының бағытымен дәл келеді.
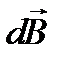векторының модулі төмендегі өрнекпен анықталады:
,
мұндағы 
- 
және векторлары арасындағы бұрыш.
Электр өрісі сияқты, магнит өрісі де суперпозиция приципіне бағынады: бірнеше токтар тудыратын қорытқы өрістің магнит индукциясы әрбір жеке токтың тудыратын өрістерінің магнит индукцияларының векторлық қосындысына тең:
.
Био-Савар-Лаплас заңының суперпозиция принципімен қоса қолдануы кейбір токтардың магнит өрістерін анықтауға мүмкіншілік береді.
1. Түзу токтың магнит өрісі:
,
мұндағы 
- ток пен қарастырылып отырған нүктенің ара қашықтығы.
2. Дөңгелек токтың центріндегі магнит өрісі:
,
мұндағы 
- дөңгелек токтың радиусы.
Магнит индукциясының сызықтары деп әр нүктесінде жүргізілген жанамалары өрістің сол нүктесіндегі магнит индукциясы векторымен бағыттас болатындай етіп жүргізілген сызықтарды атайды. Индукция сызықтарын оларға перпендикуляр орналасқан бірлік бет арқылы өтетін сызықтар саны сол жердегі векторының модуліне тең (немесе пропорционал) болатындай қоюлықпен жүргізеді.
Магнит индукциясының сызықтары әрқашан тұйықталған болады және тогы бар өткізгішті қамтиды. Үздіксіз сызықтарды иеленетін векторлық өрісті құйынды өріс деп атайды. Магнит өрісі - құйынды өріс.
Магнит өрісін сипаттау үшін магнит индукциясымен қатар басқа физикалық шаманы қолданады – ол магнит өрісінің 
кернеулігі. Вакуумде ол магнит индукция векторымен
өрнегі арқылы байланысқан.
Магнит өрісі кернеулігінің өлшем бірлігі – А/м.
Магниттік кернеу ұғымын енгізейік:
Магниттік кернеу 
контурдың пішініне тәуелді, ол контурдың бастапқы және соңғы нүктелерінің орындарымен ғана анықталмайды.
Кез келген тұйық контур бойымен алынған магниттік кернеу (
векторының циркуляциясы) нолге тең емес. Ол осы контурмен қамтылған токтардың алгебралық қосындысына тең:
мұндағы 
- пішіні кез келген контурымен қамтылған тогы бар өткізгіштердің саны. Бұл 
векторының циркуляциясы жайлы теореманы басқаша вакуумдегі магнит өрісі үшін толық ток заңы деп де атайды. векторының циркуляциясы жайлы теореманың көмегімен соленоид және тороидтың магнит өрістерін анықтауға болады.
1. Ұзындығы 
, орам саны 
соленоидтің өрісі:
.
2. Тороидтың, яғни радиусы , тор пішінді өзекшеге оралған сақина тәрізді катушканың, өрісі:
,
мұндағы - орамдар саны.
Магнит өрісінің осы өрісте орналасқан 
ток элементіне әсер ететін 
күші:
.
векторының бағытын сол қол ережесі бойынша анықтауға болады: егер сол қолдың алақанын оған векторы кіретіндей, ал ашылған төрт саусақты өткізгіштегі токпен бағытталатындай етіп орналастырса, онда тік бұрышқа қайырылған бас бармақ токқа әсер ететін күштің бағытын көрсетеді. Ампер күші деп аталатын осы күштің модулі мына өрнектің көмегімен анықталады
,
мұндағы 
- 
және векторлары арасындағы бұрыш. арақашықтықта жатқан, бойларында 
және 
тогы бар екі өзара параллель өткізгіштер бір бағыттағы ток өткен жағдайда бір-біріне тартылады да, қарама-қарсы бағытталған ток өткен жағдайда бір-бірінен тебіледі:
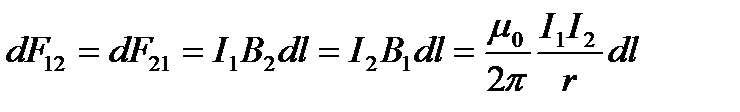
Магнит өрісінде 
жылдамдықпен қозғалатын 
электр зарядына әсер етуші күшті Лоренц күші деп атайды:
.
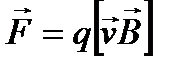Лоренц күшінің бағыты сол қол ережесі бойынша анықталады: егер сол қолдың алақанын оған векторы кіретіндей, ал ашылған төрт саусақты векторымен бағытталатындай етіп орналастырса, онда тік бұрышқа қайырылған бас бармақ оң зарядқа әсер ететін күштің бағытын көрсетеді.
Лоренц күшінің модулі:
,
мұндағы 
- 
және 
векторларының арасындағы бұрыш.
