Базис Уолша определён на интервале от 0 до 1. Дискретная модель исходного сигнала для этого интервала реализована и использовалась ранее в М-функции cosob(t,Um,Uo). При выборе количества временных отсчётов должно быть выполнено условие деления нацело их числа на число функций Уолша, кратное степени двойки. Таким образом, количество временных отсчетов должно удовлетворять соотношению length(t)/Ng = целое, где Ng=2M. Вычисления проводятся по М-функции WalBas(fname,Np,Ng,varargin) при различном числе отсчётов, их результаты представлены на рисунке 4.10.
| function [A,S,dS]=WalBas(fname,Np,Ng,varargin) % [A,S,dS]=WalBas(fname,Np,Ng,Par) | ||
| t=linspace(0,1,Np); s=feval(fname,t,varargin{:}); for i=1:Ng+1 w(i,:)=wal(i-1,t); end A=w*s/length(t); figure(1) subplot(311) stem(0:Ng,A) | S=A'*w; subplot(312) plot(t,s,t,S) s1=cosob(t,2,1); dS=S(:)-s1(:); dS1=s(:)-s1(:); subplot(313) plot(t,s1,t,dS) Err=std(dS) OtnErr=Err/sqrt(sum(s.^2)/length(s)) | |

| 
| |
Рисунок 4.10 – Спектр-диаграммы и временные зависимости сигнала в базисе Уолша
Ошибки разложения в базисе Уолша
N = 16 D = 0.0437à 10.9%
N = 96 D = 0.0685à 16.5 %
N = 256 D = 0.0682à 16.5 %
N = 512 D = 0.0682à 16.4 %
Коэффициенты разложения в базисе Уолша
N= 16 0.1968 -0.0000 -0.1968 0.0000 0.1968 0.0000 -0.1968 -0.0000 0.0423
N= 96 0.2158 -0.0000 -0.2158 0.0000 0.1826 -0.0000 -0.1826 0.0000 0.0213
N=256 0.2171 0.0000 -0.2171 -0.0000 0.1825 0.0000 -0.1825 -0.0000 0.0200
N=512 0.2176 -0.0000 -0.2176 0.0000 0.1824 -0.0000 -0.1824 0.0000 0.0196
Результаты расчётов при числе точек дискретизации более 16 (N = 96, 256, 512) практически не отличаются. Совпадение числа точек дискретизации и числа гармоник обеспечивает наименьшую ошибку при этом количестве базовых функций Уолша. Ошибки разложения в Уолша больше в 8–10 раз, чем в гармоническом и в 1.5–2.5 раза в чебышевском базисе и чуть меньше ошибок в МОБ.
Согласно выражению (4.2) записывается М-функция cosobsm(t,Um,Uo,Sm) расчёта смещённого сигнала в заданном вектором t количестве равноотстоящих точек. Величина смещения по-прежнему равна четверти периода.
Ошибки разложения в базисе Уолша
N = 16 D = 0.0685 à 16.5 % – исходный сигнал,
N = 16 D = 0.0011 à 0.3 % – смещённый сигнал,
N = 256 D = 0.0682 à 16.4 % – смещённый сигнал.
Коэффициенты разложения в базисе Уолша
Исх(16) 0.1968 -0.0000 -0.1968 0.0000 0.1968 0.0000 -0.1968 -0.0000 0.0423
Исх(256) 0.2171 0.0000 -0.2171 -0.0000 0.1825 0.0000 -0.1825 -0.0000 0.0200
Смещ. 0.2171 0.2171 -0.0020 -0.0020 -0.1824 -0.1824 0.0004 0.0004 0.0200
Смещение исходного сигнала в базисе Уолша существенно изменяет амплитудный спектр, уменьшаются также ошибки разложения при числе отсчётов, равном числе функций базиса Уолша (рисунок 4.11).

| 
|
Рисунок 4.11 – Спектр-диаграммы и временные зависимости сигнала в базисе Уолша
для смещённого сигнала
Дискретная модель суммы исходного сигнала и нормального белого шума на интервале (0,1) реализована в М-файле cosobsh(t,Um,Uo,Sigma). Величина sigma (СКО шума) выбирается равной D256 и 10D256 (рисунок 3.12)
Ошибки разложения в базисе Уолша
N = 256 D256 = 0.0685 à 16.5 % – исходный сигнал,
N = 256 D1 = 0.0698 à 16.6 % – исходный сигнал + слабый шум (s = D256);
N = 256 D2 = 0.1632 à 20.3 % – исходный сигнал + сильный шум (s = 10D256).
Коэффициенты разложения в базисе Уолша
Исход. 0.2171 0.0000 -0.2171 -0.0000 0.1825 0.0000 -0.1825 -0.0000 0.0200
s = D256 0.2176 0.0050 -0.2199 0.0009 0.1867 0.0003 -0.1811 0.0003 0.0225
s=10D256 0.2220 0.0496 -0.2445 0.0086 0.2248 0.0026 -0.1688 0.0025 0.0444
| 
|
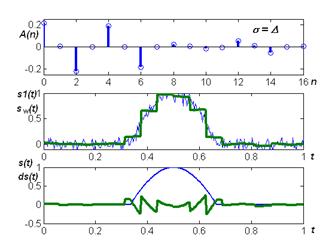
Рисунок 4.12 – Спектр-диаграммы и временные зависимости сигналов в базисе Уолша
при различных уровнях шумовой составляющей
Аддитивный нормальный шум несущественно изменяет спектральную диаграмму (основные отличия наблюдаются у высокочастотных составляющих) и влияет на уровень ошибок восстановления. Увеличение уровня шума в 10 раз приводит к возрастанию ошибок восстановления в 1.3 раза.




