Ниже приведен вариант выполнения основных пунктов задания 3, полученный с использованием математического пакета MATLAB. В качестве примера сигнала выбран один период «обрезанной косинусоиды» (рисунок 2.2), приведённый к временному масштабу (0, 1).
4.2.1 Дискретная модель сигнала s(t)
Поскольку временной интервал задан в границах от 0 до 1, то аналитический вид исходного сигнала будет равен
(4.1)
где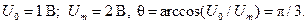 
Период сигнала задан и равен T= 1.
Согласно выражению (4.1) записывается М-функция расчёта сигнала в заданном вектором t количестве равноотстоящих точек (рисунок 4.1).
function s=cosob(t,Um,Uo)
% s = cosob(t,Um,Uo)
% t - вектор текущего времени
% Um - амплитуда
% Uo - уровень отсечки
| if nargin == 1 Um = 1; Uo = 0; elseif nargin == 2 Uo = 0; end teta = acos(Uo/Um); tg = teta/(2*pi); n = length(t); t1 = t-0.5; s = zeros(n,1); for i = 1:n if abs(t1(i)) < tg s(i)=-Uo+Um*cos(2*pi*t1(i)); end end |
Рисунок 4.1 – График исходного сигнала и М-файл его дискретной модели
Задавая вектор t в виде t256=linspace(0,1,256); и обращаясь к М-функции s256=cosob(t256,2,1);, получим 256 равноотстоящих отсчётов исходного сигнала на интервале (0, 1). Система гармонических базисных функций в тех же временных точках интервала (0, 1) составляется по командам (16 гармоник и одна постоянная):
for k=1:17
cs256(k,:)=cos((k-1)*2*pi*t256);
sc256(k,:)=sin((k-1)*2*pi*t256);
end
Далее по одной из гармонических функций определяется множитель, равный элементу (шагу) интегрирования,:
Mcs256=1/cs256(2,:)*cs256(2,:)';
Msc256=1/sc256(2,:)*sc256(2,:)';.
Поскольку вектор отсчётов сигнала и базисная система определены, то с помощью матричного перемножения вычисляются косинусная и синусная составляющие спектра сигнала:
a256=cs256*s256*Mcs256;
b256=sc256*s256*Msc256;
а также его амплитудный и фазовый спектры:
A256=sqrt(a256.^2+b256.^2);
P256=atan(b256./a256);,
которые выводятся в командное окно по команде [A256’; P256’]. На рисунке 4.2 представлены амплитудный спектр сигнала при числе точек N = 512 и отклонения от него при N = 256 и N = 100.
Рисунок 4.2 – Амплитудный спектр и отклонения от него при меньшем числе точек
Более точно изменение спектральных составляющих при различном количестве точек дискретизации представлено в таблице.
N= 100 0.4270 0.3831 0.2704 0.1355 0.0272 0.0272 0.0312 0.0098 0.0098
N= 256 0.4325 0.3879 0.2735 0.1368 0.0274 0.0274 0.0313 0.0098 0.0098
N= 512 0.4343 0.3895 0.2746 0.1373 0.0275 0.0275 0.0314 0.0098 0.0098
N = ¥ 0.4361 0.3910 0.2757 0.1378 0.0276 -0.0276 -0.0315 -0.0098 0.0098
Перед вычислением сигнала, представленного суммой гармонических составляющих, необходимо уменьшить в два раза коэффициент a 0 (здесь a256(1)):
a256(1)=a256(1)/2;
а затем сложить матричные произведения спектров и базисных функций:
S256 = a256'*cs256* +b256'*sc256;.
Вектор ошибки представления сигнала вычисляется по команде
dS256 = s256(:) – S256(:);,
а величина СКО – по команде
sigma256 = std(dS).
Относительная ошибка вычисляется по команде
Osh256 = sigma256/sqrt(sum(s256.^2)/length(s256)).
СКО разложения сигнала по гармоническому базису уменьшаются обратно пропорционально количеству отсчётов сигнала:
sigma100 sigma200 sigma256 sigma512
0.0091 0.0058 0.0057 0.0049 – абсолютная СКО,
2.2 1.4 1.4 1.2 – относительная СКО (%).
На представленных ниже временных графиках (рисунок 4.3) для повышения наглядности ошибки разложения увеличены в 10 раз. Наибольшее отклонение наблюдается около точек резкого изменения величины сигнала.
Рисунок 4.3 – Временные зависимости ошибок гармонического представления
4.2.2 Дискретная модель смещённого сигнала sсм(t)
Так как смещение равно четверти периода, т.е. 0.25, то аналитическое выражение сигнала имеет вид:
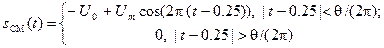(4.2)
где 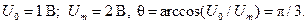Период сигнала задан и равен T= 1.
Согласно выражению (4.2) записывается М-функция cosobsm(t,Um,Uo,Sm) расчёта смещённого сигнала в заданном вектором t количестве равноотстоящих точек. Результаты расчёта спектральных составляющих:
