Амплитудный спектр

Без см 0.4325 0.3879 0.2735 0.1368 0.0274 0.0274 0.0313 0.0098 0.0098

Со см. 0.4326 0.3910 0.2735 0.1378 0.0273 0.0276 0.0313 0.0098 0.0098

Фазовый спектр

Без см 0 0 0 0 0 0 0 0 0

Со см. 0 -1.5708 0 1.5708 0 1.5708 0 1.5707 0

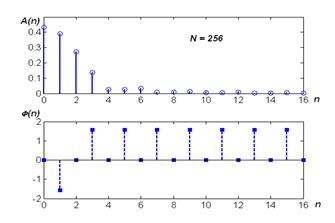
Сравнение спектров смещённого и исходного сигнала подтверждает теорему о сдвиге во временной области, согласно которой изменение положения сигнала влияет только на фазовый спектр смещённого сигнала. Величина фазового сдвига равна angle(exp(-j*pi/2)) => -p/2, но из-за небольших вычислительных ошибок около точки разрыва фаза перескакивает от -p/2 к +p/2 и обратно. Поскольку спектры практически совпадают, то и ошибки представления сигнала суммой гармоник также одинаковы для смещённого и исходного сигналов (рисунок 4.4).

Рисунок 4.4 – Спектральные диаграммы и временные зависимости для смещённого сигнала

4.2.3 Дискретная модель зашумлённого сигнала s _Ш (t)

Исходный сигнал на фоне аддитивного нормального белого шума определяется формулой:

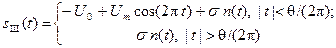(4.3)

Согласно выражению (4.3) записывается М-функция cosobsh(t,Um,Uo,Sigma) расчёта зашумлённого сигнала в заданном вектором t количестве равноотстоящих точек. Шум моделируется с помощью функции randn(length(t),1), величина СКО задается дважды: сначала равной СКО представления сигнала суммой 16 гармоник, затем десятикратной её величиной, например,

[Ash10,Psh10,Ssh10]=Fourier(@cosobsh,256,16,2,1,0.057);

где М-функция Fourier(@signal,Np,Ng,Um,Uo,sigma) вычисляет и строит амплитудный Ash10 и фазовый Psh10 спектры, а также гармоническое представление Ssh10 сигнала, представленного М-функцией signal, в Np временных точках с использованием Ng гармоник. Входные параметры Um, Uo, sigma являются параметрами М-функции signal.

Результаты расчёта спектральных составляющих:

Амплитудный спектр

Исход 0.4325 0.3879 0.2735 0.1368 0.0274 0.0274 0.0313 0.0098 0.0098

s = D 0.4326 0.3882 0.2737 0.1361 0.0277 0.0275 0.0317 0.0101 0.0096

s =10D 0.4333 0.3903 0.2748 0.1301 0.0309 0.0288 0.0353 0.0141 0.0084

Фазовый спектр

Исход 0 0 0 0 0 0 0 0 0

s = D 0.0101 0.0096 0.0132 0.0055 0.0053 0.0076 0.0036 0.0671 0.0313

s =10D 0 -0.0079 0.0127 0.0050 -0.0013 -0.0979 0.1344 0.4989 0.3650

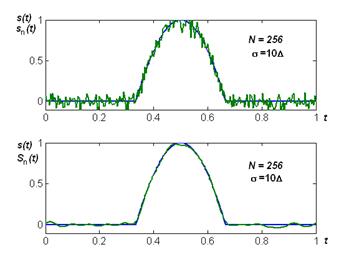
Анализ таблицы выявляет отчётливое увеличение разброса («дрожание») спектральных коэффициентов с возрастанием их номера, особенно у фазового спектра. Представленные на рисунке 4.5 временные графики показывают резкое возрастание (в 10 раз) шумовой «дорожки» у исходного сигнала и существенное её сглаживание синтезированного гармонического сигнала. Таким образом, можно избавляться от высокочастотных шумов при учёте нескольких (два – три десятка) спектральных коэффициентов ряда Фурье.

Рисунок 3.5 – Временные зависимости сигнала с аддитивным нормальным шумом

Величина ошибок при увеличении sigma в 10 раз возросла с 0.0077 до 0.0549, что в относительном масштабе составляет 1.8 % и 13.1 % соответственно.

4.2.4 Представление сигналов в базисе Чёбышева

Дискретная модель сигнала s(t) должна быть определена на интервале (-1,1). Поскольку интервал задан в границах от -1 до 1, то аналитический вид исходного сигнала примет вид:

(4.4)

где 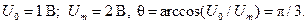Период сигнала в этом случае равен T= 2.

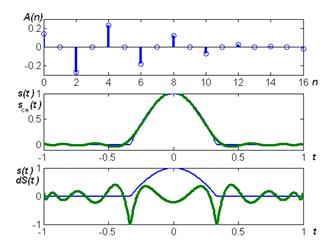
Согласно выражению (4.4) записывается М-функция cosinob(t,Um,T,Uo) расчёта сигнала в заданном вектором t количестве равноотстоящих точек (рисунок 4.6). Там же представлены спектральная диаграмма и временные зависимости синтезированной функции и ошибок разложения по чебышевскому базису.

Вычисления проводятся по функции Tchebysh(fname,Np,Ng,varargin) с фактическими параметрами [A,S,dS]=Tchebysh(@cosinob,256,16,2,2,1); для исходного и смещённого вариантов

function [A,S,dS]=Tchebysh(fname,Np,Ng,varargin) % [A,S,dS]=Tchebysh(fname,Np,Ng,Par)

t=linspace(-1,1,Np); s=feval(fname,t,varargin{:}); dt=t(8)-t(7); ct=tchebort(Ng,t); at=ct*s*dt; A=at; x=sqrt(1-t.*t); figure(1) subplot(311) stem(0:Ng,at) for i=0:Ng tc(i+1,:)=tcheb(i,t); end tc1=tc(2:Ng+1,:); at1=at(2:Ng+1,1); S=at1'*tc1; S=S+at(1); subplot(312) plot(t,s,t,S) dS=s(:)-S(:); subplot(3,1,3) plot(t,s,t,dS*10) Err=std(dS) OtnErr=Err/sqrt(sum(s.^2)/... length(s))

Рисунок 4.6 – Спектр-диаграммы и временные зависимости сигнала в чебышевском базисе

Ошибки разложения в чебышевском базисе

N = 100 D = 0.0263 à 6.4 %

N = 256 D = 0.0257 à 6.2 %

N = 512 D = 0.0255 à 6.1 %

Коэффициенты разложения в чебышевском базисе

N=100 0.1402 0.0000 -0.2681 -0.0000 0.2335 0.0000 -0.1830 -0.0000 0.1255

N=256 0.1403 0.0000 -0.2683 -0.0000 0.2336 0.0000 -0.1829 -0.0000 0.1253

N=512 0.1403 0.0000 -0.2683 -0.0000 0.2336 0.0000 -0.1829 0.0000 0.1253

Анализ результатов расчётов при различном числе точек дискретизации (N = 100, 256, 512) показывает, что ошибки разложения в чебышевском базисе больше в 3–5 раз, чем в гармоническом, и практически не зависят от количества этих точек.

Дискретная модель смещённого сигнала на интервале (-1,1) реализована в М-файле cosinobtsm(2,2,1,-0.5). Величина смещения по-прежнему равна четверти периода.

Ошибки разложения в чебышевском базисе

N = 256 D = 0.0257 à 6.2 % – исходный сигнал,

N = 256 D = 0.0171 à 4.1 % – смещённый сигнал.

Коэффициенты разложения в чебышевском базисе

Исход. 0.1403 0.0000 -0.2683 -0.0000 0.2336 0.0000 -0.1829 -0.0000 0.1253

Смещ. 0.1657 -0.1712 -0.1397 0.2852 -0.1504 -0.0833 0.1753 -0.0852 -0.0371

Смещение исходного сигнала существенно меняет амплитудный спектр в чебышевском базисе, ошибки разложения стали меньше в 1.5 раза по сравнению с разложением исходного сигнала.

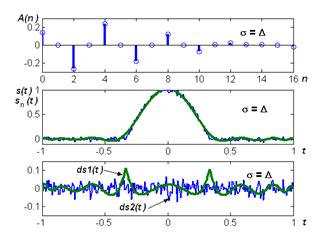
Дискретная модель суммы исходного сигнала и нормального белого шума на интервале (-1,1) реализована в М-файле cosinobtsh(2,2,1,sigma). Величина sigma (СКО шума) выбирается равной D₂₅₆ и 10D₂₅₆. Спектры и графики показаны на рисунке 4.7.

Ошибки разложения в чебышевском базисе

N = 256 D₂₅₆ = 0.0257 à 6.2 % – исходный сигнал,

N = 256 D1 = 0.0258 à 6.2 % – исходный сигнал + слабый шум (s = D₂₅₆);

N = 256 D2 = 0.0520 à 10.1 % – исходный сигнал + сильный шум (s = 10D₂₅₆).

Коэффициенты разложения в чебышевском базисе

Исход. 0.1403 0.0000 -0.2683 -0.0000 0.2336 0.0000 -0.1829 -0.0000 0.1253

s = D₂₅₆ 0.1410 -0.0023 -0.2671 0.0001 0.2369 0.0005 -0.1812 -0.0004 0.1243

s=10D₂₅₆0.1473 -0.0232 -0.2568 0.0009 0.2672 0.0050 -0.1657 -0.0043 0.1146

Рисунок 4.7 – Спектр-диаграммы и временные зависимости сигналов в чебышевском базисепри различных уровнях шумовой составляющей

Аддитивный нормальный шум почти не изменяет спектральную диаграмму (отличия наблюдаются у высокочастотных составляющих) и несущественно влияет на уровень ошибок восстановления. Увеличение уровня шума в 10 раз приводит к возрастанию ошибок восстановления в 1.6 раза.