Структурная схема САР приведена на рисунке 3.1, где
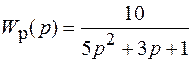. (3.1)
Рисунок 3.1 – Структурная схема САР
Требуется определить:
– коэффициенты статической ошибки C 0, скоростной ошибки C 1 и ошибки от ускорения C 2.
Для нахождения указанных коэффициентов необходимо найти передаточную функцию ошибки по выражению (2.3), то есть
.
Итак
,
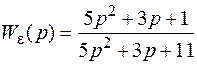на основе выражений (2.4) имеем, что
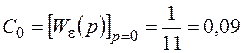
Для нахождения C 1 необходимо найти первую производную от W e(p) по правилу:
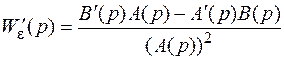, (3.2)
где B (p) – полином в числителе передаточной функции;
A (p) – полином в знаменателе.
Тогда
Итак
. (3.3)
Тогда
.
Вторая производная от передаточной функции ошибки
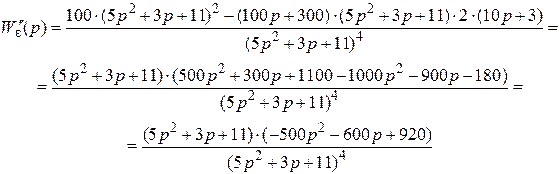
Отсюда
.
Итак
C 0 = 0,09; C 1 = 0,25; C 2 = 0,69.
Тогда
.
3.2 Построение кривой переходного процесса методом
типовых ТВЧХ
Пусть передаточная функция САР имеет вид
, (3.4)
где k = 2 – коэффициент передачи;
T 1 = 1; T 2 = 2; T 3 = 4 – постоянные времени.
Требуется:
– построить кривую переходного процесса методом типовых ТВЧХ;
– определить прямые оценки качества регулирования.
Раскроем скобки в выражении (3.4) и подставим значения k, T 1, T 2, T 3:
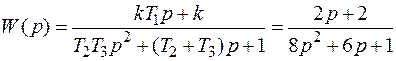. (3.5)
Получим выражение для расчета вещественной частотной характеристики P (w), заменив в (3.5) p на j w
Отсюда
.
Результаты расчета P (w) приведены в таблице 3.1, а ее график на рисунке 3.2.
Таблица 3.1 – Значения P (w)
| w | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,5 | +¥ | |||
| P (w) | 1,01 | 0,97 | 0,49 | 0,23 | 0,1 | 0,03 | -0,01 | -0,02 | -0,02 | -0,02 | -0,01 |
Аппроксимируем кривую P (w) прямолинейными отрезками. В итоге получаем три типовые ТВЧХ, характеристики которых приведены в таблице 3.2, а сами ТВЧХ приведены на рисунке 3.3.
Таблица 3.2 – Характеристики ТВЧХ
| Трапеция | ri | w di | w пi | Hi |
| I | 1,5 | 0,15 | 0,3 | 0,5 |
| II | 0,4 | 0,3 | 0,5 | 0,6 |
| III | 0,12 | 0,5 | 0,8 | 0,625 |
В таблицах 3.3, 3.4, 3.5 соответственно приведены значения для переходных процессов единичных ТВЧХ, взятых при заданных значениях наклонов Hi из таблицы приложения А, а также значения реальных кривых переходных процессов, полученных для каждой ТВЧХ по выражениям (2.14).
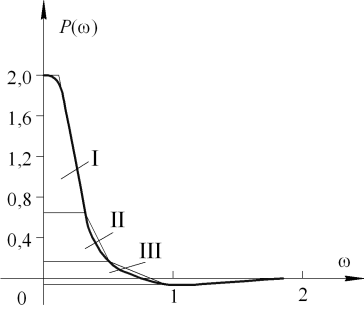
Рисунок 3.2 – Вещественная частотная характеристика
Рисунок 3.3 – ТВЧХ
Таблица 3.3 – Значения переходного процесса для ТВЧХ I
| t табл | h 11(t) | t | h 1(t) |
| 0,0 | 0,00 | 0,0 | 0,00 |
| 0,5 | 0,240 | 1,7 | 0,36 |
| 1,0 | 0,461 | 3,3 | 0,69 |
| 1,5 | 0,665 | 5,0 | 1,00 |
| 2,0 | 0,831 | 6,7 | 1,25 |
| 2,5 | 0,967 | 8,3 | 1,45 |
| 3,0 | 1,061 | 10,0 | 1,59 |
| 3,5 | 1,115 | 11,7 | 1,67 |
| 4,0 | 1,141 | 13,3 | 1,71 |
| 4,5 | 1,138 | 15,0 | 1,71 |
| 5,0 | 1,117 | 16,7 | 1,68 |
| 5,5 | 1,090 | 18,3 | 1,64 |
| 6,0 | 1,051 | 20,0 | 1,58 |
| 6,5 | 1,018 | 21,7 | 1,53 |
| 7,0 | 0,992 | 23,3 | 1,49 |
| 7,5 | 0,974 | 25,0 | 1,46 |
| 8,0 | 0,966 | 26,7 | 1,45 |
| 8,5 | 0,964 | 28,3 | 1,45 |
| 9,0 | 0,968 | 30,0 | 1,45 |
| 9,5 | 0,975 | 31,7 | 1,46 |
| 10,0 | 0,982 | 33,3 | 1,47 |
| 10,5 | 0,988 | 35,0 | 1,48 |
Продолжение таблицы 3.3
| t табл | h 11(t) | t | h 1(t) |
| 11,0 | 0,993 | 36,7 | 1,49 |
| 11,5 | 0,996 | 38,3 | 1,49 |
| 12,0 | 0,997 | 40,0 | 1,50 |
Таблица 3.4 – Значения переходного процесса для ТВЧХ II
| t табл | h 12(t) | t | h 2(t) |
| 0,0 | 0,000 | 0,00 | |
| 0,5 | 0,255 | 0,10 | |
| 1,0 | 0,490 | 0,20 | |
| 1,5 | 0,706 | 0,28 | |
| 2,0 | 0,878 | 0,35 | |
| 2,5 | 1,010 | 0,40 | |
| 3,0 | 1,100 | 0,44 | |
| 3,5 | 1,145 | 0,46 | |
| 4,0 | 1,158 | 0,46 | |
| 4,5 | 1,141 | 0,46 | |
| 5,0 | 1,107 | 0,44 | |
| 5,5 | 1,064 | 0,43 | |
| 6,0 | 1,020 | 0,41 | |
| 6,5 | 0,982 | 0,39 | |
| 7,0 | 0,957 | 0,38 | |
| 7,5 | 0,944 | 0,38 | |
| 8,0 | 0,941 | 0,38 | |
| 8,5 | 0,948 | 0,38 | |
| 9,0 | 0,961 | 0,38 | |
| 9,5 | 0,977 | 0,39 | |
| 10,0 | 0,993 | 0,40 | |
| 10,5 | 1,005 | 0,40 | |
| 11,0 | 1,014 | 0,41 | |
| 11,5 | 1,017 | 0,41 | |
| 12,0 | 1,018 | 0,41 | |
| 12,5 | 1,015 | 0,41 | |
| 13,0 | 1,012 | 0,40 | |
| 13,5 | 1,008 | 0,40 |
Таблица 3.5 – Значения переходного процесса ТВЧХ III
| t табл | h 13(t) | t | h 3(t) |
| 0,5 | 0,259 | 0,625 | 0,03 |
| 1,0 | 0,505 | 1,250 | 0,06 |
| 1,5 | 0,722 | 1,875 | 0,09 |
| 2,0 | 0,899 | 2,500 | 0,11 |
| 2,5 | 1,030 | 3,125 | 0,12 |
| 3,0 | 1,116 | 3,750 | 0,13 |
| 3,5 | 1,158 | 4,375 | 0,14 |
| 4,0 | 1,162 | 5,000 | 0,14 |
| 4,5 | 1,138 | 5,625 | 0,14 |
| 5,0 | 1,097 | 6,250 | 0,13 |
| 5,5 | 1,050 | 6,875 | 0,13 |
| 6,0 | 1,001 | 7,500 | 0,12 |
| 6,5 | 0,965 | 8,125 | 0,12 |
| 7,0 | 0,941 | 8,750 | 0,11 |
| 7,5 | 0,931 | 9,375 | 0,11 |
| 8,0 | 0,934 | 10,000 | 0,11 |
| 8,5 | 0,948 | 10,625 | 0,11 |
| 9,0 | 0,967 | 11,250 | 0,12 |
| 9,5 | 0,987 | 11,875 | 0,12 |
| 10,0 | 1,006 | 12,500 | 0,12 |
По данным, приведенным в таблицах 3.3, 3.4, 3.5 строим переходные процессы h 1(t), h 2(t), h 3(t), которые приведены на рисунке 3.4.
Строим реальную кривую переходного процесса y (t) путем графического суммирования переходных процессов h 1(t), h 2(t), h 3(t) (рисунок 3.4).
Определяем прямые оценки качества регулирования:
– время регулирования t р = 18,75 сек.;
– время нарастания переходного процесса t н = 8,5 сек.;
– время достижения первого максимума t max = 12,5 сек;
– перерегулирование
,
где 
.
Рисунок 3.4 – Кривая переходного процесса и оценки
качества регулирования
Так как переходной процесс не является колебательным, то число колебаний N = 0.
Полученная область допустимых отклонений выделена на рисунке 3.4 штриховкой.
