Для расчета прямых оценок качества регулирования необходимо уметь строить кривые переходного процесса. В работе для этого используются два метода:
– приближенный метод трапецеидальных вещественных частотных характеристик (ТВЧХ);
– метод разностных уравнений.
2.3.1 Метод трапецеидальных вещественных частотных
характеристик (ТВЧХ)
Типовая ТВЧХ, приведенная на рисунке 2.4, определяется тремя параметрами:
r 0 – высота трапеции;
w d – интервал равномерного пропускания частот;
w п – общий интервал пропускания частот.
Рисунок 2.4 – Типовая трапецеидальная вещественная
частотная характеристика
Если r0 = 1, w п = 1, то типовая ТВЧХ называется единичной. Единичной типовой ТВЧХ соответствует переходный процесс h 1(t), значения которого приведены в таблице приложения А для каждого значения коэффициента наклона
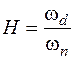. (2.13)
Величина коэффициента наклона H характеризует наклон типовой ТВЧХ. Переход от переходного процесса h 1(t) к реальному переходному процессу h (t) осуществляется по выражениям:
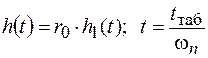, (2.14)
где t – реальное время.
Кривая на основе типовых ТВЧХ строится следующим образом:
1. По заданной передаточной функции САР строится вещественная частотная характеристика P (w), приведенная на
рисунке 2.5.
Рисунок 2.5 – Вещественная частотная характеристика
2. Вещественная частотная характеристика P (w) разбивается на типовые ТВЧХ. Для этого P (w) заменяется мало отличающейся от нее ломаной кривой, состоящей из сопрягающих друг с другом прямолинейных отрезков (на рисунке 2.5 ломаная кривая АВСDЕ). Через точки сопряжения (на рисунке 2.5 точки В, С, D) проводятся прямые, параллельные оси частот. Таким образом, P (w) заменяется определенным числом ТВЧХ:
. (2.15)
На рисунке 2.5 P (w) заменена двумя ТВЧХ: АВСF и FDЕ0.
3. Для каждой трапеции определяются ее параметры: ri, Hi и w пi. Если трапеция направлена вниз (на рисунке 2.5 трапеция FDЕ0), то ri берется со знаком минус.
4. По таблице А.1 в приложении А в зависимости от Hi для каждой ТВЧХ находятся значения, соответствующие кривой переходного процесса h 1 i (t).
5. По выражениям (2.14) определяются значения для реальных кривых переходного процесса hi (t), на основе которых строятся их графики (рисунок 2.6).
Рисунок 2.6 – Реальная кривая и кривые типовых переходных процессов
6. Значения кривых типовых переходных процессов складываются с учетом их знаков, и в итоге получается реальная кривая переходного процесса y (t).
