Параметры колебательного процесса и их определение

Любые отклонения физического тела или параметра его состояния, то в одну, то в другую сторону от положения равновесия называется колебательным движением или просто колебанием. Колебательное движение называется периодическим, если значения физических величин, изменяющихся в процессе колебаний, повторяются через равные промежутки времени.

Гармоническими называются колебания, совершающиеся по закону sin или cos.

s=Asin(ωt+j_о), s=Аcos(ωt+j_o)

Они совершаются под действием квазиупругих сил, т.е. сил, пропорциональных смещению F=–kx

Основными характеристиками колебаний являются:

1. Смещение (s) – это расстояние, на которое отклоняется колеблющаяся система в данный момент времени, от положения равновесия.

2. Амплитуда (А) – максимальное смещение.

3. Период (Т) – время одного полного колебания.

4. Линейная частота (ν) – это число колебаний в единицу времени, измеряется в Гц – это одно колебание в сек. ν=1/Т.

5. Циклическая или круговая частота (ω) рад/сек. Она связана с линейной частотой следующей зависимостью: ω =2πν.

6. Фаза колебания (j) характеризует состояние колеблющейся системы в любой момент времени: j= ωt+j₀, j₀ – начальная фаза колебания.

 

 

 

26. Колебания подпрыгивания кузова вагона. Трение в рессорном подвешивании отсутствует.

Рассмотрим систему с линейным (вязким) сопротивлением в РП

где .

Уравнение подпрыгивания и галопирования идентичны как в левых так и в правых частях, с учетом этого рассмотрим случай колебания подпрыгивания когда профиль пути синусоидальный (i =1), трение в РП отсутствует ().

Тогда уравнение (1) примет вид

Решение этого неоднородного уравнения составляет

.

где - общее решение однород ур-я (без правой части);

- частное решение неоднор. уравнен.

Общее решение однор. ур-я получим при решении ур-я собствен колебаний без трения:

где Е,φ – амплитуда и нач фаза собственных колебаний, определяемые из нач. условия. ω – собственная круговая частота колебаний, рад/с.

Частное решение найдём в форме правой части

,

где М₁ – const подлежащая определению,

р₁ – круговая частота вынужденных колебаний.

Определяем производные и подставим в выражение (2):

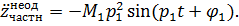
Это уравнение является тождеством, когда + .

Отсюда .

Полное решение всего неоднородного уравнения приобретает вид

 

27.Колебания подпрыгивания кузова вагона. Демпфирование умеренное <ω

Решение. Движение подчиняется закону:

Множитель обуславливает периодическое движение. Множитель обуславливает затухание колебаний с ростом t. Период колебаний:

;

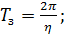
Где 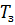период затухания колебаний

-круговая частота затухающих собственных колебаний.

Период остается неизменным все рассматриваемое время

Темп затухания колебаний определим как отношение двух последовательных размахов за один период (декремент)

Отсюда следует, что затухание колебаний происходит по закону геометрической прогрессии.

28.Колебания подпрыгивания кузова вагона. Демпфирование критическое v=ω

v=ω Движение теряет периодичность и становится лимитационным (т.е. колебаний нет). Демпфирование соотв. этому случаю называется критическим демпфированием.

По нормам проектирования рациональными величинами будут:

- для вертикальных колебаний β=(0,3…0,4)β_кр;

- для гор. β=(0,3…0,4)β_кр.