Для вывода дифференциальных уравнений колебаний кузова вагона как механической системы с пятью степенями свободы необходимо дифференцировать сложные функции кинетической энергии К, потенциальной энергии П и функции рассеивания Ф относительно переменных: 
(здесь 
). Сложные функции соответственно равны:
Тогда получим:
Подставим значения производных в уравнение:
Получаем математическую модель колебаний кузова вагона как механической системы с пятью степенями свободы в виде системы обыкновенных дифференциальных уравнений с постоянными коэффициентами:
Рассматриваем вагон с низким расположением центра тяжести (принимаем h=0), что позволит разорвать взаимосвязь колебаний боковой качки и поперечного относа. Уравнения колебаний кузова приобретает вид:
– поперечного относа;
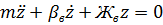– подпрыгивания;
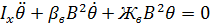– боковой качки;
– галопирование;
– виляние.
Полученная математическая модель колебаний подрессоренных частей вагона позволяет определить рациональные параметры рессорного подвешивания тележек.
33. Расчётная схема для получения математической модели вынужденных колебаний вагона
Расчётная схема предлагает два положения вагона: равновесное в начальный момент времени и текущее положение в произвольное время. Предполагаем что четырёхосный вагон движется самостоятельно по рельсовому пути. Кузов вагона считаем абсолютно твёрдым телом с массой m и моментом инерции относительно поперечной центральной оси 
. Рессорные комплекты подвешивания рассматриваем в качестве упруго-вязких связей с суммарными жёсткостью 
и коэффициентом демпфирования 
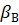. База вагона – 2L, база тележки 2l, высота центра тяжести кузова относительно плоскости его опирания на рессорные комплекты – h. Массой неподрессоренных частей вагона пренебрегаем, путь считаем абсолютно жёстким.
Схема является плоской. Здесь учитывается то, что колёсные пары вагона проходят одни и те же неровности пути в разное время, когда вертикальные возмущающие перемещения колёс в произвольный момент времени различны. Мы рассматриваем плоскую схему, когда неровности правого и левого рельсов симметричны. Такая схема достаточно проста и адекватна для решения поставленных задач.
34. Определение сил в системе “вагон-путь” при получении математической модели вынужденных колебаний.
Система имеет 3 степени свободы, определяемые координатами x, y, z. при известной величине система имеет две степени свободы.
Уравнение равновесия по пр. Даламбера: 
,
где 
- вес подрессоренных частей, 
, 
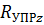– суммарная вертикальная реакция упругих элементов рессорного подвешивания вагона
, 
- вертикальные деформации рессорного подвешивания первой и второй тележки.
, 
Реакция демпфирующих элементов находится по формуле:
Подставив эти выражения в формулу для нахождения реакции упругих элементов получим:
- приведённое линейное возмущающее перемещение ходовых частей
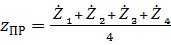
Сила инерции находится:
Подставляем найденные величины в уравнение равновесия, и получим уравнение вынужденных колебаний подпрыгивания.
