Все химические реакции можно разделить на 2 группы: реакции необратимые, т.е. протекающие до полного израсходования хотя бы одного из реагирующих веществ, и реакции обратимые, в которых ни одно из реагирующих веществ не расходуется полностью. Это связано с тем, что обратимая реакция может протекать как в прямом, так и в обратном направлении. Классическим примером обратимой реакции может служить реакция синтеза аммиака из азота и водорода:
N2 + 3 H2 ⇆ 2 NH3.
В момент начала реакции концентрации исходных веществ в системе максимальны; в этот момент максимальна и скорость прямой реакции. В момент начала реакции в системе ещё отсутствуют продукты реакции (в данном примере – аммиак), следовательно, скорость обратной реакции равна нулю. По мере взаимодействия исходных веществ друг с другом, их концентрации уменьшаются, следовательно, уменьшается и скорость прямой реакции. Концентрация же продукта реакции постепенно возрастает, следовательно, возрастает и скорость обратной реакции. Через некоторое время скорость прямой реакции становится равна скорости обратной. Это состояние системы называется состоянием химического равновесия. Концентрации веществ в системе, находящейся в состоянии химического равновесия, называются равновесными концентрациями. Количественной характеристикой системы в состоянии химического равновесия является константа равновесия.
Для любой обратимой реакции a A + b B+... ⇆ p P + q Q + … выражение константы химического равновесия (К) записывается в виде дроби, в числителе которой находятся равновесные концентрации продуктов реакции, а в знаменателе – равновесные концентрации исходных веществ, причём концентрация каждого вещества должна быть возведена в степень, равную стехиометрическому коэффициенту в уравнении реакции.
Например, для реакции N2 + 3 H2 ⇆ 2 NH3.
Следует иметь в виду, что в выражение константы равновесия входят равновесные концентрации только газообразных веществ или веществ, находящихся в растворённом состоянии. Концентрация твёрдого вещества считается постоянной и не записывается в выражение константы равновесия.
CO2 (газ) + C (тв.) ⇆ 2CO (газ)
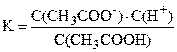
CH3COOH(раствор) ⇆ CH3COO–(раствор) + H+(раствор)
Ba3(PO4)2 (тв.) ⇆ 3 Ba2+(насыщ. раствор) + 2 PO43–(насыщ. раствор) К=C3(Ba2+)·C2(PO43–)
Существует два наиболее важных типа задач, связанных с расчётом параметров равновесной системы:
1) известны начальные концентрации исходных веществ; из условия задачи можно найти концентрации веществ, прореагировавших (или образовавшихся) к моменту наступления равновесия; в задаче требуется рассчитать равновесные концентрации всех веществ и численную величину константы равновесия;
2) известны начальные концентрации исходных веществ и константа равновесия. В условии нет данных о концентрациях прореагировавших или образовавшихся веществ. Требуется рассчитать равновесные концентрации всех участников реакции.
Для решения подобных задач необходимо понимать, что равновесную концентрацию любого исходного вещества можно найти, отняв от начальной концентрации концентрацию прореагировавшего вещества:
С равновесная = С начальная – С прореагировавшего вещества.
Равновесная концентрация продукта реакции равна концентрации продукта, образовавшегося к моменту наступления равновесия:
С равновесная = С образовавшегося продукта.
Таким образом, для расчёта параметров равновесной системы очень важно уметь определить, сколько к моменту наступления равновесия прореагировало исходного вещества и сколько образовалось продукта реакции. Для определения количества (или концентрации) прореагировавшего и образовавшегося веществ проводятся стехиометрические расчёты по уравнению реакции.
Пример 6.1 Начальные концентрации азота и водорода в равновесной системе N2 + 3H2 ⇆ 2 NH3 соответственно равны 3 моль/л и 4 моль/л. К моменту наступления химического равновесия в системе осталось 70% водорода от его первоначального количества. Определить константу равновесия данной реакции.
Для того чтобы рассчитать константу равновесия, необходимо сначала рассчитать равновесные концентрации всех участников реакции и затем подставить их в выражение константы равновесия.
Из условия задачи следует, что к моменту наступления равновесия прореагировало 30% водорода (задача 1 типа):
4 моль/л H2 – 100%
х моль/л H2 – 30%
х = 1,2 моль/л = С прореаг.(H2)
Как видно из уравнения реакции, азота должно было вступить в реакцию в 3 раза меньше, чем водорода, т.е. С прореаг.(N2) = 1,2 моль/л: 3 = 0,4 моль/л. Аммиака же образуется в 2 раза больше, чем прореагировало азота:
Собразов.(NH3) = 2 × 0,4 моль/л = 0,8 моль/л
Равновесные концентрации всех участников реакции будут таковы:
Сравн.(H2)= Cнач.(H2) - Cпрореаг.(H2) = 4 моль/л – 1,2 моль/л = 2,8 моль/л;
Сравн.(N2)= Cнач.(N2) – Cпрореаг.(N2) = 3 моль/л – 0,4моль/л = 2,6 моль/л;
Сравн.(NH3) = Собразов.(NH3) = 0,8 моль/л.
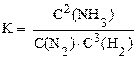Константа равновесия = 
.
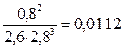Пример 6.2 Рассчитать равновесные концентрации водорода, йода и йодоводорода в системе H2 + I2 ⇆ 2 HI, если известно, что начальные концентрации H2 и I2 равны 5 моль/л и 3 моль/л соответственно, а константа равновесия равна 1.
Следует обратить внимание, что в условии этой задачи (задача 2 типа) в условии ничего не говорится о концентрациях прореагировавших исходных веществ и образовавшихся продуктов. Поэтому при решении таких задач обычно концентрация какого-нибудь прореагировавшего вещества принимается за икс.
Пусть к моменту наступления равновесия прореагировало x моль/л H2. Тогда, как следует из уравнения реакции, должно прореагировать x моль/л I2, и образоваться 2x моль/л HI. Равновесные концентрации всех участников реакции будут таковы:
Сравн.(H2) = Cнач.(H2) – Cпрореаг.(H2) = (5 – x) моль/л;
Сравн.(I2) = Cнач.(I2) – Cпрореаг.(I2) = (3 – x) моль/л;
Сравн.(HI) = Собразов.(HI) = 2x моль/л.
Далее необходимо подставить выраженные через икс равновесные концентрации в формулу для константы равновесия и решить полученное уравнение.
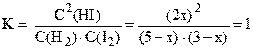
4x2 = 15 – 8x + x2
3x2 + 8x – 15 = 0
x1 = –3,94 x2 = 1,27
Физический смысл имеет только положительный корень x = 1,27.
Следовательно, Сравн.(H2) = (5 – x) моль/л = 5 – 1,27 = 3,73 моль/л;
Сравн.(I2) = (3 – x) моль/л = 3 – 1,27 = 1,73 моль/л;
Сравн.(HI) = 2x моль/л = 2·1,27 = 2,54 моль/л.
Далее (таблица 7) приводятся условия задач по теме «Химическое равновесие» для самостоятельного решения.
