1932 жылы. Найквист радиотехника күшейткіштерін зерттеу үшін, ал содан кейін А.В. Михайлов 1938 жылы. Автоматты реттеу жүйесін зерттеу үшін жиілікті амплитуда – фазалы критериді ұсынды, ол тұйықталған жүйенің ажыратылған жүйенің амплитуда – фазалы сипаттамасы бойынша тұрақтылығы жөнінде түсініктеме береді.
Амплитуда – фазалық тұрақтылық критериясы келесі түрде түрленеді (құрылады): егер ажыратылған тұрақты жүйенің амплитуда – фазалық сипаттамасы координатасы (-1, j0) нүктесін қамтымаса, онда тұрақталған жүйе тұрақты.
Келтірілген түрдегі амплитуда – фазалы критериясы ажыратылған жүйе тұрақты болған кезде ғана әділетті, ал амплитуда – фазалық сипаттама теңдеуінде бөліміндегі полином дәрежесі алымындағы полином дәрежесінен кіші.
Ажыратылған жүйе, егер тұрақты үзбелерден тұрса – апериодты, тұрақты тербелісті үзбелерден тұрған және ең кем дегенде бір интегралдаушы үзбеден тұрған кезде тұрақты. Бұл тікелей құрылымдық схемаға кіретін үзбелерді қарастырумен орнатылады.
Амплитуда – фазалық сипаттамсы координатасы (-1, j0) нүктесін қамтитынын келесі түрде анықтауға болады. (-1, j0) нүктесінен көмекші АВ векторын амплитуда – фазалық сипаттамаға өткіземіз (5.7. сурет) 
0- ден 
ке дейін өзгерген кезде осы вектордың ұшы В амплитуда – фазалы сипаттама бойынша жылжиды, ал бүкіл АВ векторы А нүктесінің айналасымен кейбір бұрышқа бұрылады. Егер АВ векторының барлық бұрылу бұрышы 0- ден ке дейін өзгерген кезде нөльге тең болса, онда сипаттама А (-1, j0) нүктесін қамтымайды және жүйе тұрақты (5.7. сурет, 
). Егер осы бұрылу бұрышы нөльге тең болса, онда сипаттама А (-1, j0) нүктесін қамтиды және жүйе тұрақсыз (5.7. сурет,б).
Рис. 5 – 7. Амплитудно-фазовые характеристики статических систем:
а – устойчивой; б – неустойчивой.
Астатикалық жүйелердің беріліс функциясы интегралдаушы үзбенің бар болуының арқасында 
көбейткіші бар, ал амплитуда – фазалық сипаттама теңдеуінде сәйкесінше 
көбейткіші пайда болады. 
болған кезде ажыратылған жүйенің амплитуда – фазалық сипаттамасы шексіздікке кетеді (5.8. суреттегі ON1M1 қисығы). Осы қисық А (-1, j0) нүктесін қамтитынын дәлелдеу үшін амплитуда – фазалық сипаттамасының айналу бейнесі болып табылатын қосымша ON1N2 қисығын тұрғызады, және ON1N2 сипаттамасын ON1N2 сипаттамамен қоса отырып, центрі координа басында орналасқан шексіз үлкен радиусты доғаны жүргіземіз. Егер алынған тұрақталған қисық бойынша АВ векторының ұшымен енді жүрсек, онда оның А нүктесінің айналасында бұрылу бұрышының қосындасы тұйықталмаған жүйе тұрақты ма немесе тұрақсыз екенін анықтайды. Егер осы бұрыш нөльге тең болса (5.8. сурет, ), онда жүйе тұрақты. 5.8, суреттегі б АВ векторының соммалы бұрылу бұрышы 
ге тең, сәйкесінше тұйықталған жүйе тұрақсыз.
Ажыратылған жүйенің күшейту коэффициентін жоғарлатқан кезде амплитуда – фазалық сипаттама өзінің түрін өзгертпей «тармақталады», яғни сипаттаманың координата өзгертпей, «тармақталады», яғни сипаттаманың координата басынан бастаған әрбір нүктеге дейінгі ара қашықтығы бірдей санға үлкейеді. Амплитуда – фазалық сипаттаманың бұл қасиеті кейбір күрделі жағдайларда басқа тұрақтылық критериясының көмегімен жасау күрделі болатын жүйенің параметрлерін дұрыс таңдап алуға мүмкіндік береді.
Қарапайым бірконтурлы жүйенің амплитуда – фазалық критериясының физикалық критериясының физикалық тұжырымы амплитуда – фазалық сипаттаманы анықтаудан шығады. Амплитуда – фазалық сипаттама өзінше ұзындығы ажыратылған жүйенің шығыс пен кіріс сигналдардың амплитудалар қатынасына тең, айналдырушы векторларды береді, ал нақты өсьтегі оң бағыттағы вектордан пайда болған бұрыш осы сигналдардың фазасының жылжуын көрсетеді.
Нақты өсьтің теріс таңбалы бөлігінің амплитуда – фазалық сипаттамасының қиылысу нүктесіндегі фазалар жылжуы 1800-қа тең, және сәйкесінше, шығыс сигнал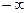 
пен (-1, j0) нүктесінің арасында орналасқан, бұл шығыс амплитуданың кірісіне қатынасы бірден үлкен екенін білдіреді, яғни осы жиіліктегі жүйенің күшею коэффициенті бірден үлкен. Осындай жүйеде тұйықталу кезінде онда нақты өсьті сипаттаманың қиылысу нүктесіне сәйкес өсіңкі амплитудалы мен жиілікті бос еркін тербелістер жүреді.
Егер нақты өсьті сипаттаманың қилысу нүктесі координатаның бас нүктесі мен (-1, j0) нүктесінің арасында орналласа, онда жүйені күшейту коэффициенті бос еркін тербеліс онда өшеді.
5.8. Сурет. Астатикалық жүйелердің амплитуда – фазалық сипаттамалары
тұрақты; б-тұрақсыз;
Көпконтурлы жүйелердегі түрлену мен амплитуда – фазалық критерия талқыламасы күрделірек.
Ажыратылған тұрақты жүйенің амплитуда – фазалық сипаттамасы 5.9 суретте көрсетілген түрдегі жағдайды қарастырайық.
Күшею коэффициенті өзгерген кезде әркез жаңа қисықтарды қосу міндетті емес, сызбаның масштабын ауыстыру жеткілікті. Егер күшею коэффициенті жеткілікті аз болса, онда координатасы (-1, j0) нүкте А1күйге келеді, жүйе тұрақты. Ол А2 күйге келгенде, онда тұйықталған жүйе тұрақтылық шегіне келеді күшею коэффициентін әрі қарай жоғарлатқан кезде жүйе тізбектеліп тұрақсыз (A3 күйі), тұрақты (A5 күйі) және тағы тұрақсыз (А7 күйі) болады. (-1, j0) нүктесі A4 және A6 күйге келгенде жүйе тұрақтылық шегінде орналасады.
5.9. Сурет. Ерекше түрде амплитуда – фазалық сипаттама
Мұнда амплитуда – фазалық сипаттама дәлелдеусіз келтірілген. Дәлелдемесімен танысқысы келгендер (24, 28, 42) әдебиеттер қорынан алуға болады.
Бұл критериде жүйені ажырату зерттеу жұмысын едәуір жеңілдеткен кезде қиылыспалы кері байланысы жоқ жүйелер үшін пайдаланған жөн.
Сонымен қатар жүйе тұрақтылығын зерттеу мен ажыратылған жүйе тұрақсыз жағдайларда да мүмкін. Дегенмен ол аса күрделі.
Мысал. Амплитуда – фазалы критерийдің көмегімен 4.1 берілген автоматты реттеу жүйесінің тұрақтылығын зерттейміз; (4.19) өрнегі бұл жүйенің ажыратылған күйдегі беріліс функциясын береді. Алымындағы жақшаларды ашып, көбейтеміз және ұқсас мүшелерді келтіреміз, содан алатынымыз
(5.12)
Белгілеулер (4.29)- да келтірілген.
(5.12)-ге (5.40)-ғы тұрақты коэффициенттерді қойып шығып, аламыз
(5.13)
Ажыратылған жүйенің амплитуда – фазалық сипаттама теңдеуін алу үшін (5.13) өрнегіндегі p- ны 
ға айналдырамыз 
(5.14)
(5.14) өрнегінің алымымен бөлімін алымына тіркескен комплекстік санға көбейтеміз, және нақты мен жорамал бөліктерін бөліп аламыз.
(5.15)
5.2 – кесте
| ω | P(ω) | Q(ω) | ω | P(ω) | Q(ω) |
| 4,000 | 0,000 | -0,610 | -0,135 | ||
| 0,1 | 3,987 | -0,460 | -0,310 | +0.102 | |
| 0,2 | 3,850 | -0,895 | -0,093 | 0,107 | |
| 0,5 | 3,130 | -1,950 | +0,003 | 0,025 | |
| 0,7 | 2,520 | -2,370 | 0,002 | 0,008 | |
| 1,580 | -2,610 | 0,000 | 0,002 | ||
| -0,237 | -1,970 | 0,000 | 0,001 | ||
| -0,747 | -1,067 | 0,000 | 0,000 |
(5.15) өрнекке W-нің 0-ден + 
аралықтағы әртүрлі мәндерді қойып шығып P() нақты және 
жорамал бөлігінің мәндерін есептеп шығамыз. Есептің нәижелері 5.2 кестеге енгізілген, ол арқылы 5.10- суретте амплитуда – фазалы сипаттама тұрғызылған. Ол сипаттама координаттасы (-1, j0) нүктені қамтиды, және сәйкесінше, жүйе тұрақты, ол басқа тұрақтылық критерияларының көмегімен алынған нәтижелерге сәйкес келеді.
Амплитуда – фазалық сипаттама (-1, j0) нүктесі арқылы өтетін критикалық күшею коэффициентін тауып аламыз. Ол үшін (5.10. сурет) сызба маштабын өзгертеміз және координатта басынан сипаттаманың нақты өсьпен қиылысу А нүктесіне дейінгі ара –қашықтықты бір деп қабылдаймызү
Координатта басынан W=0, болған кездегі сипаттама басталатын нүктеге дейінгі кесіндіні жаңа бірліктің ұзындығына көбейтіп 
ті табамыз, ол да Михайлов критериясының көмегімен алынған нәтижелермен сәйкес келеді. Әдетте дәл сәйкестік бола, бермейді, өйткені графикалық тұрғызылғандарда кейбір қателер болады. Бірақ бұл қателіктер сызықтандыру кезінде жіберілген қателіктер шегінен шығып кетпейді, сондықтан әбден мүмкін.
5.10. Сурет. Мысалға алынған амплитуда – фазалы сипаттама
