Михайловтың тұрақтылық критериясы

 

1838 жылы А.В. Михайлов тұйықталған сызықты автоматты реттеу жүйесін зерттеу үшін өзі ұсынғанжиілікті тұрақтылық критериясын басып шығады.

Михайловтың критериясы, Гурвиц критериясы сияқты тұйықталған жүйенің сипаттамлық теңдеуін қарастырады. Осы критерияны көрсетейік (5.1) жүйесінің сипаттамалық теңдеуінің туындысы жоғары коэффициентке бөлеміз.

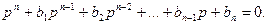(5.6)

Бұл теңдеудің жалпы жағдайда комплекстік түбірі бар

(5.7)

Түбірлерді 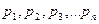арқылы белгілеп, (5.6) сипаттамлық теңдеуді мына көбейткіштерге жіктеуге болады. (5.8)

мұндағы p – еркін комплекстік сан

Комплекстік сан комплексті жазықтықта координатта басынан шығатын 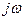вектормен берілуі мүмкін (5.2 сурет).

Вектор ұзындығы комплекстік санның модуліне, ал оң таңбалы нақты өсь бағыттағы вектордан туған бұрыш – оның аргументіне тең, егер вектор 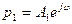көрсеткіш түрінде жазылған болса. Вектордың ұшындағы нүкте координаттары оны (5.7) түрінде жазуға мүмкіндік береді.

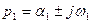
5.2. Сурет. Санның комплекстік 5.3. Сурет. Вектордың берілуі

жазықтықта берілуі

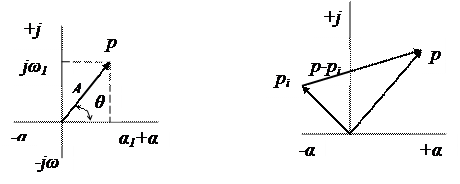
(5.8) өрнегіндегі көбейткіштер векторлар айырымын береді, ал алынған векторының ұшынан кішірейетін векторының, басына өткізілген вектормен геометрялық түрде беріледі (сурет 5.3) векторы – еркін комплекстік сан болғандықтан, таза 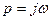жорамал түрде қабылдануы мүмкін. осы санды бейнелейтін (көрсететін) вектор жорамал өсь бағытына сәйкес келеді. (5.8) теңдеуіне кіретін көбейткіштер мына түрде болады:

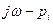(5.9)

5.4. Сурет. Вектордың комплексті жазықтықта бұрылуы

 

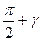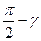нақты теріс таңбалы комплекстік тіркескен түбірлер кезіндегі бұрылу бұрыштары және , оң таңбалы нақты бөлікті түбірлер кезінд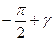е және 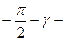ні құрайды.

(5.8) сипаттамлық теңдеуді 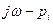түрдегі векторларды модулі көбейткіш векторларының модульдер туындысына, ал аргументі – көбейткіш векторларының аргументтер қосындысына тең жаңа векторға түрлендіру ретінде қарастыруға болады.

Сипаттамалық теңдеулеріндегі барлық нақты түбірлер бөлігі теріс тұрақты жүйедегі бұрылу бұрыштарының соммасы ге тең болады. Мұндағы теңдеудегі түбірлер саны. тіркескен комплекстік түбірлер жағдайында 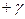және 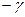қосымша бұрыштар өзара жойылып кетеді.

Сипаттамалық теңдеулерінде теріс және оң таңбалы нақты түбірлер бөлігі бар тұрақсыз жүйедегі туынды векторының бұрылу бұрышы де кіші.

Тұрақтылықты іс жүзінде осы әдіспен зерттеген кезде түбірлердің мәнін білу керек емес. Және (5.1) сипаттамалық теңдеуді (5.6) түрге келтіру де қажет емес. 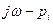түріндегі барлық векторлардың туындысы олардың (5.1) сипаттамлық теңдеулеріндегі ның орнына ні қою арқылы тікелей алуға болады, нәтижеде комплекстік функция алынады.

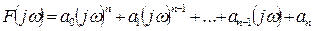(5.10)

Осы өрнектегі нақты бөлікті жорамал бөліктеп бөліп, аламыз.

(5.11)

ң бірқатар мәндерін 0–ден + ке дейінгі аралықта қоя отырып, 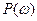мен –ң бір қатар мәндерін аламыз, олар ң әрбір мәні үшін комплекстік жазықтықтағы 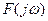векторының координаттары болып табылады. Егер барлық алынған нүктелерді толқынды қосатын болсақ, онда сипаттамлы қисық немесе Михайлов сызықтармен годографын аламыз. 0–ден + ке дейін өзгерген кезде 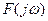векторы қандай да бір бұрышқа бұрыла отырып, өзінің ұшымен годограф бойынша орын ауыстыратын болады.

Вектордың бұрылу бұрышы ке тең болғанда жүйе тұрақты жағдайда, годограф координата басы арқылы өтпей, комплекстік жазықтықтың квадраттары арқылы өтеді (5.5. сурет, 1. қисығы). Егер жүйе тұрақсыз,болса, онда вектордың жалпы бұрылу бұрышы – ден кіші болады және годографпен нақты өсьпен кесіп өтетін ОА және ОВ кесінділер қатынасы бойынша тұрақтылық қоры жөнінді түсіндіріп бере алады. Егер ОВ ОА – мен салыстырғанда жеткілікті үлкен болса, жүйенің тұрақтылық қоры едәуір жоғары ОВ кесіндісін кішірейтумен тұрақтылық қоры төмендейді. А нүктесі болған кезде годографтың басты нүктесі болып табылады, оның абсциссасы (5.10) сипаттамалық теңдеудің бос мүшесіне санды түрде тең.

В нүктесінің абсциссасын табу үшін (5.11) теңдеулердегі 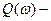дің жорамал бөлігі үшін нөль өрнекке ұмтылатын мәнін анықтайды, ал содан кейін оларды нақты бөлігінің өрнегіне қойып шығады және 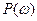мәнін есептеп шығады. 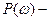ң табылған мәндері Михайлов годографының нақты өсьпен қиылысу нүктелерінің абсциссалары болып табылады.Ең кіші теріс таңбалы мән В нүктесінің абсциссасын береді.

Жүйенің жалпы күшейту коэффициентін жоғарлату кезінде Михайловтың годографы өзінің түрін өзгертпей, оң жаққа орын ауыстырады және күшейту коэффициентінің кейбір критикалық мәнінде координата басынан өтеді. Бұл жағдайда жүе тұрақтылық шегінде орналасады. күшейту коэффициентін әрі қарай жоғарлатқан кезде годограф оң жаққа орналасып квадранттар саны арқылы өтетін болады, аз ретті дифференциялды теңдеулерде жүйе тұрақсыз болады.

5.5. Сурет. Михайловтың годографы

1– төртінші ретті тұрақты жүйе

2– төртінші ретті тұрақсыз жүйе

 

Критериялық күшейту коэффициентін табу үшін (5.1) теңдеуін 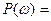0 және 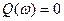болған кезде шешу қажет. Ол үшін 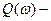ті нөльге айналдыратын мәндерін табады, және оларды 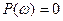кезде нақты бөлігінің теңдеуіне қоя отырып, мәнін тауып аламыз.

Егер реттеу жүйесі статикалық болса, онда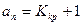

Осыдан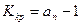

Егер реттеу жүйесі астатикалық болса, онда

Егер жүйе тұрақсыз болса, онда вектордың жалпы бұрылу бұрышы ден кіші болады және годограф квадранттар арқылы өтпейді (5.5. сурет, 2-ұисық).

Михайлов годографы, сол годографпен нақты өсьпен кесіп өтетін ОА және ОВ кесінділер қатынасы бойынша тұрақтылық қоры жөнінде түсіндіріп бере алады. Егер ОВ ОА ­– мен салыстырғанда жеткілікті үлкен болса, жүйенің тұрақтылық қоры едәуір жоғары. ОВ кесіндісін кішірейтумен тұрақтылық қоры төмендейді. А нүктесі болған кезде годографтың басты нүктесі болып табылады, оның абсциссасы (5.10) сипаттамалық теңдеудің бос мүшесіне санды түрде тең.

В нүктесінің абсциссасын табу үшін (5.11) теңдеулердегі 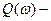дің жорамал бөлігі үшін нөль өрнекке ұмтылатын мәнін анықтайды, ал содан кейін оларды нақты бөлігінің өрнегіне қойып шығады және 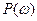мәнін есептеп шығады. 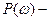ң табылған мәндері Михайлов годографының нақты өсьпен қиылысу нүтелерінің абсциссалары болып табылады. Ең кіші теріс таңбалы мән В нүктесінің абсциссасын береді.

Мысалы. Төртінші ретті сипаттамалы теңдеуі бар (5.5) жүйені Михайлов критериясының көмегімен тұрақтылыққа тексереміз.

Теңдеудегі ның орнына 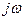санын қоямыз.

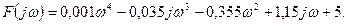
Нақты және жорамал бөліктерін бөліп аламыз.

Әртүрлі мәндерін қойып шығып, годограф нүктелерінің координаттарын аламыз (кесте 5.1) және осы нүктелердә 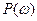, комплекстік жазықтықтардағы мысалдың масштабқа (енгіземіз) жазамыз. Оларды толқынды қисықтармен (5.5. сурет, 1 қисық) қоса отырып Михайлов годографы төрт квадрант арқылы өтеді, сәйкесінше, берілген жүйе тұрақты.

Жүйенің тұрақтылық қорын анықтаймыз. Ол үшін мәнін табамыз, ол кезде

Q ()=0

осыдан

5.1– кесте

Р ()	+5	+4,68	+2,17	-2,88	-5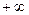
Q ()		+1,12	+2,51	+1,37	-0,64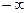

-ті теңдеудің нақты бөлігін қойып шығып, ОВ кесіндісінің шымасын анықтаймыз (5.5 сурет, қара).

Осылай, ОВ-5,4 кесіндісі ОА=5 кесіндісінен құралады.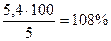

сәйкесінше, жүйенің тұрақтылық шегінде орналасқан кездегі критерикалық күшейту коэффициентін табамыз. Теңдеудің нақты және жорамал бөлігін нөльге теңестіріп, бос мүшенің мәнін табамыз

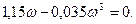
Екінші теңдеудегі мәндері жоғарыда табылған. Оларды бірінші теңдеуге қойып, аламыз

Сірә, ОА мен ОВ кесінділерінің қосындысына тең. Қарастырылып жатқан жүйе статикалық, сондықтан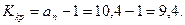

Сәйкесінше, мәндері күшею коэффициентінің мәндері 9,4- ден асып кеткен кезде, жүйе тұрақтылығын жоғалтады. Тұрақтылық шегінде орналасқан жүйе үшін Михайлов годографы 5.6 суретте көрсетілген.

 

5.6. Сурет. Критикалық күшею коэффициенті

Негізгі әдебиет: 1[150-178]; 2[127-164].

Қосымша әдебиет: 1[159-195]; 2[165-198].

Бақылау сұрақтар:

1. Қандай жұйелер тұрақты, тұрақсыз деп аталады.
2. Автоматты реттеу жүйесінің тұрақтылығы мен сипаттамалық теңдеулер түбірлерінің таңбалары арасында қандай байланыс бар.
3. Тұрақтылық критериясы дегеніміз не.
4. Гурвицтің тұрақтылық критериясын түрлендіріп беріңіз.
5. Михайловтың тұрақтылық критериясын түрлендіріп беріңіз.

№ 6 Дәрістің конспектісі

Дәрістің тақырыбы: Сызықты жүйе тұрақтылығын зерттеу. (Сызықты жүйе тұрақтылығының түсініктемесі мен жалпы шарттары. Гурвиц және Раусст алгебралық тұрақтылық критериялары. Михайлов пен Найквистің жиілікті тұрақтылық критериялары.Михайлов және Найквистің тұрақтылық критериясының жиілікті жағдайлары. Гурвиц критериясының жиілікті жағдайлары. Вышнеградскийдің критериясы, логарифмдік тұрақтылық критериясы. Тұрақтылық критериясының салыстырмалы бағалау. Тұрақтылық аймақтарын шығару Д –бөліктеу) (бөлу) әдісі. Сипаттамалық теңдеулер түбірі мен жүйе параметрлерінің, сол жүйе тұрақтылығына әсері.