Основными характеристиками методики анализа являются воспроизводимость и правильность, предел обнаружения, границы определяемых содержаний и чувствительность.
Воспроизводимость
Воспроизводимость (precision) - степень близости друг к другу независимых результатов измерений при оговоренных условиях.
Количественно воспроизводимость (или невоспроизводимость) удобнее всего описывать с помощью относительного стандартного отклонения. Чем больше величина Sr, тем воспроизводимость хуже.
Для сравнения воспроизводимости результатов двух серий анализа используют F-критерий (критерий Фишера).
Полученное значение сравнивают с критическим (табличным) при выбранном уровне значимости (обычно 0,05 или 0,01) и числе степеней свободы (f1,f2). При конкурирующей гипотезе «одна из дисперсий больше второй дисперсии» используют уровень значимости a (односторонняя постановка задачи), при конкурирующей гипотезе «дисперсии не равны между собой» используется уровень значимости a/2 (двухсторонняя постановка задачи). Если Fэксп < Fкрит, то считается, что дисперсии двух серий анализа отличаются незначимо.
Пример 10.5. При измерении рН раствора один студент получил результат 
, а второй студент - 
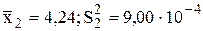. Определить, различаются ли полученные данные по воспроизводимости, если каждый студент провёл по 5 параллельных измерений.
Поскольку 
, можно сделать вывод, что полученные результаты имеют одинаковую воспроизводимость.
Правильность
Правильность (accuracy) - отсутствие систематического смещения результатов от действительного значения, отсутствие систематической погрешности.
Правильность, в отличие от воспроизводимости, является качественной характеристикой. Результат анализа может быть правильным либо неправильным.
Для проверки правильности используют следующие приёмы:
· варьирование величины пробы;
· способ «введено-найдено»;
· анализ образца различными методами - метод, выбранный для сравнения, должен быть независимым (иметь другой принцип) и давать заведомо правильные результаты;
· анализ стандартных образцов.
При проверке правильности результатов анализа приходится сравнивать средние результаты, полученные исследуемым и стандартным методом. Если установлено, что отличия между дисперсиями статистически незначимы, то это можно сделать следующим образом.
Вначале рассчитывают средневзвешенное значение дисперсии:
Затем рассчитывают экспериментальное значение t-критерия:
Если число параллельных опытов в каждой серии равно, то
Полученное значение t сравнивают с критическим значением t для выбранного уровня значимости и числа степеней свободы f = n 1 + n 2 - 2. При односторонней постановке задачи используется уровень значимости a, при двусторонней постановке задачи - a/2. Если tэксп < tкрит, то средние результаты не имеют значимых различий.
Пример 10.6. Определить отличаются ли средние результаты, полученные в примере 10.5.
Критическое значение t для a = 0,05 и f = 8 равно 2,31 (табл.2.2). Так как tэксп > tкрит, то расхождение между средними результатами статистически значимо - среднее значение рН, полученное первым студентом больше, чем полученное вторым студентом.
Предел обнаружения, предел определения и границы определяемых содержаний
Предел обнаружения (detection limit, mmin, P или Сmin, P) - наименьшее содержание аналита (масса, концентрация), которое по данной методике с заданной доверительной вероятностью (обычно P = 0,99) можно отличить от сигнала контрольного опыта.
Предел обнаружения обычно оценивается по наименьшему аналитическому сигналу (ymin), который значимо отличается от сигнала контрольного опыта, но выражается в виде массы (абсолютный предел обнаружения) или концентрации (относительный предел обнаружения). Согласно IUPAC минимальным обнаруживаемым сигналом считается такой, который превышает среднее значения сигнала контрольного опыта на 3 S последнего (рис. 10.4). Если значения аналитического сигнала контрольного опыта и минимального обнаруживаемого сигнала распределены нормально, то при расстоянии между ними 6s вероятность их перекрывания составляет всего лишь 0,13%, что вполне допустимо. Величину сигнала, превышающую среднее значение сигнала контрольного опыта на 3S, можно с вероятностью более 99% считать принадлежащей определяемому веществу.
Рис. 10.4. Предел обнаружения
Величина предела обнаружения определяется не абсолютной величиной среднего значения сигнала контрольного опыта, а его стандартным отклонением.
Предел обнаружения используется в качественном анализе. Он показывает, какое минимальное количество определяемого вещества можно обнаружить с помощью данной методики. В количественном анализе обычно используется предел определения (limit of determination). Он отличается от предела обнаружения более высокой надёжностью регистрации полезного сигнала (10S, а не 3S) и рассчитывается так же, как и предел обнаружения.
Для двух методов анализа IUPAC делает исключения: в атомно-абсорбционной спектроскопии минимальным определяемым сигналом считается оптическая плотность 0,005 (погрешность 0,0005) при использовании стандартных горелок с высотой пламени 10 см и объёме анализируемой пробы 1 мл, в спектрофотометрии пределом определения считается оптическая плотность 0,025 при погрешности измерения сигнала ±0,0025, толщине поглощающего слоя 1 см и объёме пробы 1 мл.
Диапазон определяемых содержаний - область содержаний определяемого вещества в анализируемом объекте, которые можно определить с помощью данной методики.
Область определяемых содержаний ограничивается нижней (НГОС) и верхней (ВГОС) границами определяемых содержаний. НГОС (ВГОС) считается наименьшее (наибольшее) значение определяемого содержания, которое может быть определено с погрешностью, не превышающей заданную, как правило, с Sr £ 0,33 (рис. 10.5).
Рис. 10.5. Нижняя граница определяемых содержаний
Чувствительность
Чувствительностью (коэффициентом чувствительности, S от англ. sensitivity) называется степень изменения аналитического сигнала при изменении количества вещества, обуславливающего появление этого сигнала. Другими словами, коэффициент чувствительности - это значение первой производной градуировочной функции при данном определённом содержании вещества, или, в случае линейной градуировочной функции, угловой коэффициент градуировочного графика.
Чем круче наклон графика зависимости величины аналитического сигнала от содержания определяемого вещества, тем выше чувствительность аналитической методики (рис. 10.6).
Рис. 10.6. Сравнение чувствительности двух аналитических методик
