Применение экстракции
· разделение веществ (выделение микрокомпонента, очистка макрокомпонента);
· концентрирование;
· в гибридных методах анализа (экстракционная фотометрия, экстракционная флуориметрия и др.)
· изучение различных равновесий.
ГЛАВА 10
Хемометрика (хемометрия) - химическая дисциплина, которая занимается применением математических и статистических методов для планирования и выбора оптимальных условий проведения химического эксперимента и аналитического измерения, а также получения максимума информации из химических данных.
Методы хемометрики используются на всех основных этапах химического анализа.
10.1. Приближённые вычисления и значащие цифры
Некоторые из численных величин, полученных экспериментальным путём, могут быть известны абсолютно точно (например, число таблеток, взятых для анализа), другие же (объём раствора, масса навески) всегда известны с некоторой неопределённостью. Простейшим способом описания неопределённости численной величины является понятие «значащие цифры».
Значащими называют все достоверные цифры, входящие в состав численный величины, а также первую, следующую за ними, недостоверную цифру.
При определении числа значащих цифр, входящих в состав численной величины, используют следующие правила:
· положение запятой не влияет на число значащих цифр
· нули, входящие в состав числа, могут быть как значимыми, так и незначимыми
Для того чтобы избежать проблем с определением числа значащих цифр, входящих в состав недостоверно известной величины, рекомендуется используемые численные величины записывать в виде числа, все цифры которого значимы, умноженного на десять в некоторой степени. Например, 0,05 как 5×10-2; 0,050 как 5,0×10-2 и т.д.
При вычислениях с использованием экспериментально полученных величин следует помнить, что в результате расчётов «точность» не должна искусственно повышаться, так как она определяется тем, с какой погрешностью измерены исходные величины, входящие в расчётную формулу. Существуют определённые правила, которые в большинстве случаев позволяют избежать ошибок при расчётах.
Сложение и вычитание
Перед проведением данных действий необходимо вначале все числа округлить до одинакового числа десятичных знаков - такого же как у числа с минимальным их количеством.
Сумма должна содержать столько же десятичных знаков, сколько этих знаков содержится у числа с наименьшим их количеством.
Возможна и другая последовательность действий: вначале проводят сложение (вычитание) неокруглённых чисел, а затем уже полученный ответ округляют до требуемого числа десятичных знаков.
При сложении или вычитании чисел, записанных в степенной форме, их вначале приводят к числу с наибольшим показателем степени, а затем поступают так же, как и для обычных чисел. Например
1,03×102 + 5,2×103 = 0,103×103 + 5,2×103 = 5,3×103
Деление и умножение
Строгий подход к определению правильного числа значащих цифр, которое должно остаться в произведении или в частном, предполагает сравнение относительных недостоверностей исходных величин и получаемых результатов. В большинстве случаев, однако, можно ограничиться следующим правилом: результат деления или умножения должен иметь столько же значащих цифр (не десятичных знаков!), сколько их содержится в наименее точно известном числе.
Другие операции
При возведении в степень, равную n, относительная недостоверность результата будет в n раз больше, чем недостоверность исходной величины. При извлечении квадратного корня (n = 1/2) относительная недостоверность уменьшается в два раза, кубического (n = 1/3) - в три раза, поэтому можно, например, считать, что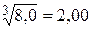 
и т.д. При логарифмировании число значащих цифр обычно увеличивают. При потенцировании (взятии антилогарифма) число значащих цифр, наоборот, уменьшают. Например:
lg 0,01 (или lg 1×10-2) = -2,0
10-2,0 = 0,01 (или 1×10-2)
