I уровень
1.1. Представьте число в тригонометрической и показательной форме. Изобразите его на плоскости:
1) 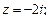 2)
2)  3)
3) 
4)  5)
5)  6)
6) 
1.2. Представьте комплексное число в алгебраической форме:
1) 
2) 
3) 
1.3. Используя тригонометрическую формулу комплексного числа, выполните действия:
1) 
2) 
3) 
4) 
5) 
6) 
7) 
1.4. Возведите в степень:
1)  2)
2) 
3)  4)
4) 
1.5. Представив комплексные числа 

 в тригонометрической форме, вычислите
в тригонометрической форме, вычислите 
1.6. Вычислите корни из комплексных чисел и дайте геометрическую интерпретацию их значений:
1)  2)
2)  3)
3)  4)
4) 
5)  6)
6)  7)
7)  8)
8) 
1.7. Выполните действия, результат запишите в алгебраической форме:
1)  2)
2)  3)
3) 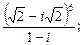 4)
4) 
5)  6)
6) 
1.8. Решите уравнение:
1)  2)
2) 
3)  4)
4) 
5)  .
.
1.9. Изобразите на комплексной плоскости множество точек, для которых:
1)  2)
2)  3)
3) 
4) 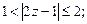 5)
5)  6)
6) 
7) 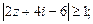 8)
8) 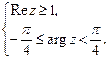
II уровень
2.1. Представьте число в тригонометрической и показательной форме:
1)  2)
2) 
3)  4)
4) 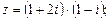
5)  6)
6) 
2.2. Даны комплексные числа 
 Представив их в тригонометрической форме, вычислите:
Представив их в тригонометрической форме, вычислите:
1)  2)
2)  3)
3)  4)
4) 
2.3. Используя тригонометрическую форму комплексного числа, выполните действия:
1)  2)
2) 
3)  4)
4) 
2.4. Возведите в степень, результат запишите в алгебраической форме:
1)  2)
2) 
3)  4)
4) 
2.5. Вычислите корни, а результат изобразите на комплексной плоскости:
1)  2)
2)  3)
3) 
4)  5)
5)  6)
6) 
2.6. Решите уравнение:
1)  2)
2) 
3)  4)
4) 
5)  6)
6)  ;
;
7)  .
.
2.7. Изобразите на комплексной плоскости множество точек, для которых:
1)  2)
2) 
3)  4)
4) 
5)  6)
6) 
III уровень
3.1. Представьте в алгебраической и тригонометрической формах комплексные числа и выполните действия:
1)  2)
2) 
3)  4)
4) 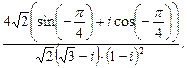
3.2. Пусть 
 Найдите действительные значения a и b, для которых
Найдите действительные значения a и b, для которых 
3.3. Изобразите множество точек комплексной плоскости, координаты х и у которых удовлетворяют условию

3.4. Найдите комплексное число z, удовлетворяющее уравнению

3.5. Определите, при каких действительных значениях х и у комплексные числа 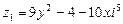 и
и  являются сопряженными.
являются сопряженными.
3.6. Решите уравнение:
1) 
2)  3)
3)  4)
4) 
3.7. Изобразите на комплексной плоскости множество точек, удовлетворяющих следующим условиям:
1)  2)
2) 
3)  4)
4) 
3.8. Найдите z 6, если 
3.9. Найдите a и b, если известно, что комплексное число  является корнем уравнения
является корнем уравнения 
3.10. Комплексное число z удовлетворяет условию  Найдите z 18.
Найдите z 18.
Ответы к заданиям для самостоятельного решения
Раздел 7.1.
I уровень
1.1. 1)  2) 4,26 рад.; 3)
2) 4,26 рад.; 3)  4)
4)  5) 0,47 рад.
5) 0,47 рад.
1.2. 1) 630º; 2) 495º; 3) 540º; 4) 36,7º; 5) 207,9º.
1.3. 1)  2)
2)  3)
3)  4)
4) 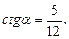
1.4. 1)  2) 1; 3)
2) 1; 3)  4)
4)  5) 0,25; 6) 1; 7)
5) 0,25; 6) 1; 7)  8)
8) 
9) 1; 10) 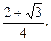
1.5. 1) 1 и  2) 5 и 0; 3) 7 и
2) 5 и 0; 3) 7 и 
1.6. 1) 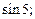 2)
2) 
1.8. 1) 2; 2)  3)
3)  4)
4)  5)
5)  6) 1.
6) 1.
II уровень
2.1. 1) 
 2)
2) 
3) 
2.2. 1) >0; 2) >0; 3) >0; 4) >0; 5) <0.
2.3. 1) 98; 2)  3) 2; 4)
3) 2; 4)  5) 2; 6)
5) 2; 6)  7)
7)  8) 0,5;
8) 0,5;
9) 1; 10)  11) 4.
11) 4.
2.5. 1) 2; 2)  3)
3)  4)
4)  5) 1; 6)
5) 1; 6)  7) 1;
7) 1;
8) 
2.6. 
III уровень
3.2. 1)  ; 2)
; 2)  .
.
3.3. 1) 0; 2) 2; 3)  4) 1; 5)
4) 1; 5) 
6) 
3.4. 
3.5. 
3.6. 1.
Раздел 7.2.
I уровень
1.1. 1)  2)
2)  3)
3)  4)
4)  5) 0;
5) 0;
6)  7)
7)  8)
8)  9)
9)  10)
10) 
1.2. 1)  2)
2)  3) 0; 4)
3) 0; 4)  5)
5) 
6)  7)
7)  8) 0,125.
8) 0,125.
1.4. 1)  2)
2) 
1.5. 1)  2)
2) 
1.7. 1) 0; 2) 0.
1.8. 1)  2)
2) 
3) 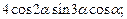 4)
4) 
5) 
1.9. 1)  2)
2) 
1.10. 1)  2)
2)  3) 1; 4)
3) 1; 4)  5)
5) 
II уровень
2.1. 1) 
 2)
2) 
3) 
 4) 1,5; 5)
4) 1,5; 5) 
2.2. 1) 2; 2)  3)
3)  4)
4)  5) 1;
5) 1;
6) 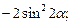 7)
7) 
8) 
2.4. 1) 1; 2)  3) 0; 4)
3) 0; 4)  5)
5) 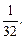
2.5. 1) 2, –1; 2) 1; 0,25; 3) 
 4)
4) 

2.7. 1)  2)
2) 
3) 
2.8. 1) 0; 2) 
2.10. 1) 1; 2)  3)
3)  4)
4)  5)
5) 
III уровень
3.1. 1) 2; 2) 82; 3)  4)
4)  5)
5) 
3.2. 1) 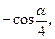 при
при 
 при
при 
2)  3)
3)  4) 1; 5)
4) 1; 5) 
3.4. 1) 2; 2)  3) 2.
3) 2.
3.6. 1) 1; 0,5; 2) 12, –4; 3) 
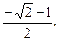
3.7. рациональным.
3.8. 
3.9. 1) 4; 2) 
3.11. 1)  2)
2)  3)
3)  4)
4) 
5)  6)
6) 
Раздел 7.3.
I уровень
1.1. 1) D (у)=3); 2) 
3)  4)
4) 
1.2. 1)  2)
2)  3)
3) 
4)  5)
5) 
1.3. 1) нечетная; 2) нечетная; 3) функция общего вида;
4) четная; 5) четная.
1.4. 1)  2)
2)  3)
3)  4)
4) 
5)  6)
6)  7)
7)  8)
8) 
II уровень
2.1. 1)  2)
2) 
3)  4)
4) 
2.2. 1)  2)
2)  3)
3) 
4)  5)
5) 
2.3. 1) четная; 2) функция общего вида; 3) четная;
4) функция общего вида; 5) нечетная; 6) нечетная;
7) четная.
2.4. 1)  2)
2)  3)
3)  4)
4) 
III уровень
3.1. 1)  2)
2) 
3)  4)
4)  5)
5) 
3.2. 1)  2)
2)  3)
3) 
4)  5)
5) 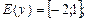 6)
6) 
3.3. 1) нечетная; 2) четная; 3) четная; 4) четная.
4. 1)  2)
2)  3)
3)  4) не существует.
4) не существует.
3.5. 1) 
2) 
3.8.  .
.
Раздел 7.4.
I уровень.
1. 1)  2)
2)  3)
3)  4)
4)  5)
5)  6)
6) 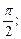
7)  8) 0.
8) 0.
1.3. 1)  2)
2)  3)
3)  4)
4)  5)
5) 
6)  7)
7)  8) 2; 9)
8) 2; 9)  10) 0.
10) 0.
1.4. 1) 
2) 
II уровень.
2.1. 9)  ; 10)
; 10)  ; 11)
; 11)  .
.
2.3. 1) 0; 2)  3)
3)  4)
4)  5)
5) 
2.4. 1)  2)
2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  .
.
III уровень.
3. 1. 1)  2)
2) 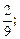 3)
3)  4)
4)  5) 0; 6) 0; 7)
5) 0; 6) 0; 7) 
8)  9)
9) 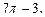
3.2. 1)  2)
2)  3)
3)  4)
4)  5)
5) 
6)  7)
7)  ; 8)
; 8)  ; 9)
; 9)  .
.
3.3. 1)  ; 2)
; 2)  ; 3)
; 3)  ;
;
4)  ; 5)
; 5)  .
.
Раздел 7.5.
I уровень
1.1. 1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ; 7)
; 7)  ;
;
8)  .
.
1.2. 1) 

2) 



3) 



4) 



5) 

6) 



7) 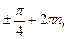

8) 



9) 



10) 



11) 

12) 



13) 



14) 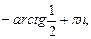



15) 

16) 

17) 



18) 

19) 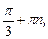

20) 



21) 

22) 

23) 



24) 

25) 



26) 

27) 



28) 



29) 

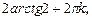

II уровень
2.1.1) 



2) 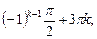

3) 



4) 



5) 



6) 

7) 



8) 

9) 



10) 



11) 



12) 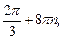



13) 

14) 

15) 

16) 

17) 



18) 



19) 



20) 

21) 

22) 
23) 





24) 



25) 

26) 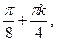


27) 
28) 
29) 

30) 
III уровень
3.1.1) 



2) 

3) 

4) 

5) 



6) 

7) 



8) 

9) 

10) 





11) 

12) 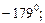
13) 

14) 

15) 

16) 

17) 

18) 

19) 
20) 5.
3.2. 1) 
 2)
2) 
 3) 2; 4) 1.
3) 2; 4) 1.
3.3. 1)  ; 2)
; 2)  ; 3)
; 3)  .
.
Раздел 7.6.
I уровень
1.1. 1) 

2) 

3) 

4) 

5) 

6) нет решений.
II уровень
2.1.1) 

2) 

3) 

4) 

5) нет решений;
6) 

III уровень
3.1.1) 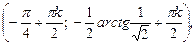

2) 

3) 
 4) нет решений;
4) нет решений;
5) 
 ; 6)
; 6) 
 .
.
Раздел 7.7.
I уровень
1.3. 3)  4)
4) 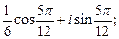 5)
5) 
6)  7)
7) 
1.4. 1) i; 2)  3)
3)  4)
4) 
1.5. 
1.8. 1) 

2) 


3) 
4) 
5)  .
.
II уровень
2.1. 3) 
2.2. 1) 
2) 
3)  4)
4) 
2.3. 1)  2)
2)






