Формулировки определений и теорем, перечисленных выше в п. 1-35.
Теоремы с изложением доказательства:
1. Теорема о единственности предела сходящейся последовательности.
2. Теорема о локальной ограниченности функции, имеющей конечный предел.
3. Теоремы о пределе суммы, произведения и частного функций (доказательство для функций или последовательностей по выбору).
4. Теорема о пределе сложной функции.
5. Теорема о знакопостоянстве функции, имеющей ненулевой предел.
6. Теорема о предельном переходе в неравенстве (доказательство для функций или последовательностей по выбору).
7. Теорема о пределе промежуточной функции (доказательство для функций или последовательностей по выбору).
8. Теорема о дифференцируемости сложной функции.
9. Теорема о дифференцируемости обратной функции.
10. Теорема Ферма.
11. Теорема Ролля.
12. Теорема Лагранжа.
13. Теорема Коши.
14. Теорема Бернулли – Лопиталя для предела отношения двух бесконечно малых функций.
15. Вывод формулы Тейлора с остаточным членом в форме Пеано и в форме Лагранжа (формулировка и доказательство соответствующих теорем).
16. Необходимое и достаточное условия возрастания и убывания дифференцируемой функции.
17. Достаточное условие локального экстремума функции по ее первой производной.
18. Достаточное условие локального экстремума функции по ее второй производной.
19. Достаточное условие выпуклости дважды дифференцируемой функции.
20. Необходимое условие для существования точек перегиба графика функции.
21. Достаточное условие для существования точек перегиба графика функции.
Типовой экзаменационный билет
1. Докажите теорему о единственности предела сходящейся последовательности.
2. Докажите теорему Бернулли – Лопиталя для предела отношения двух бесконечно малых функций.
3. Вычислите предел 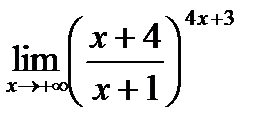 .
.
4. Исследуйте функцию 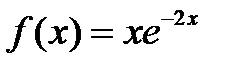 и постройте ее график.
и постройте ее график.
Литература
Основная литература (ОЛ)
1. Морозова В.Д. Введение в анализ. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2005. – 408 с.
2. Иванова Е.Е. Дифференциальное исчисление функций одного аргумента. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2001. – 408 с.
3. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. Т. 1. – М.: Интеграл-Пресс, 2006. – 416 с.
4. Сборник задач по математике для втузов. Ч. 1. Линейная алгебра и основы математического анализа: Учеб. пособие для втузов / Под ред. А.В. Ефимова, Б.П. Демидовича. – М.: Наука, 1993. – 478 с
Дополнительная литература (ДЛ))
1. Ильин В.А., Позняк Э.Г. Основы математического анализа. Ч. 1. – 4-е изд., перераб. и доп. – М.: Наука, 1982. – 616 с.
2. Кудрявцев Л.Д. Курс математического анализа. В 3-х т. Т. 1. – М.: Высшая школа, 1988. – 718 с.
3. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. – М.: Наука, 1988. – 431 с.
4. Задачи и упражнения по математическому анализу для втузов / Под ред. Б.П. Демидовича. – М.: Астрель, 2003. – 472 с.
5. Вся высшая математика: Учебник для втузов: В 6 т. / Краснов М.Л., Киселев А.И., Макаренко и др. – Т. 1. – М.: Эдиториал УРСС, 2000. – 328 с.
Методические пособия
1. Галкин С.В. Математический анализ. Методические указания по материалам лекций для подготовки к экзамену в первом семестре. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2004. – 116 с.
2. Грибов А.Ф., Котович А.В., Минеева О.М. Кривые на плоскости, заданные параметрически и в полярной системе координат. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2004.
3. Казанджан Э.П. Исследование функций и построение графиков. – М.: Изд-во МГТУ им. Н.Э. Баумана, 1995.
4. Ильичев А.Т., Кузнецов В.В., Фаликова И.Д. Графики элементарных функций. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2004.
5. Соболев С. К., Ильичев А. Т. Исследование и построение плоских кривых, заданных параметрически и в полярных координатах. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2004. – 80 с.
6. Казанджан Э.П., Казанджан Г.П. Вычисление пределов. – М.: Изд-во МГТУ им. Н.Э. Баумана, 1995.
7. Кузнецов В.В., Коньков А.А., Соболев С.К. Множества и элементы математической логики. – М.: МГТУ, 1989. – 48 с.
8. Под ред. Ивановой Е.Е. Введение в анализ.-М., МГТУ, 1990.-85с.
9. Казанджан Г.П., Казанджан Э.П. Рабочий справочник по математике. – М., МГТУ, 2002.
10. Михайлова Т.Ю., Поляшова Р.Г., Титов К.В. Исследование свойств функций и построение графиков. Формула Тейлора и ее приложения. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2002.
11. Казанджан Э.П. Графики. Сборник задач с примерами решений по исследованию функций и построению графиков. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2004.
12. Дуров В.В., Мастихин А.В., Савин А.С. Пределы и непрерывность функций. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2004. – 62 с.
Рекомендуемые Интернет-сайты:
1. Иванков П.Л. Конспект лекций по математическому анализу // http://mathmod.bmstu.ru/
МАТЕМАТИЧЕСКИЙ АНАЛИЗ






