МОДУЛЬ 1. Элементарные функции и пределы
Домашнее задание № 1 «Элементарные функции и их графики»
Срок выдачи – 1-я неделя
Домашнее задание № 1 включает поиск области определения функции, исследование функции на четность/нечетность, элементарные преобразования графиков функций, построение эскизов графиков функций.
Срок сдачи – 4 неделя
Типовой вариант домашнего задания № 1
Задача 1. Найти область определения функции  .
.
Задача 2. Исследовать функцию  на четность (нечетность).
на четность (нечетность).
Задача 3. Используя элементарные преобразования, построить эскизы графиков следующих функций:
а)  , б),
, б), 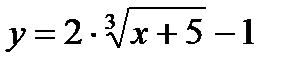 в)
в)  ,
,
г)  , д)
, д)  .
.
Задача 4. Построить эскиз графика рациональной функции  , исследуя его расположение относительно оси абсцисс и асимптот.
, исследуя его расположение относительно оси абсцисс и асимптот.
Задача 5. Используя правила построения графика суммы, произведения, частного или композиции двух функций, построить эскиз графика функции 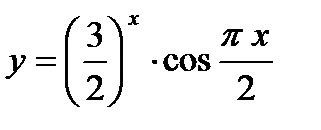 .
.
Домашнее задание № 2 «Пределы»
Срок выдачи – 4-я неделя
Домашнее задание № 2 посвящено теории пределов. Требуется умение пользоваться определением предела по Коши; вычислять пределы функций, используя различные методы и приемы; сравнивать бесконечно малые (бесконечно большие) функции; исследовать функцию на непрерывность и классифицировать точки разрыва.
Срок сдачи – 8 неделя
Типовой вариант домашнего задания № 2
Задача 1. Для заданной последовательности  и числа
и числа  доказать, что
доказать, что  , определив для каждого
, определив для каждого  число
число  , такое, что
, такое, что  для всех
для всех  . Заполнить таблицу:
. Заполнить таблицу:

| 0,1 | 0,01 | 0,001 |

|
Задача 2. Вычислить следующие пределы:
а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д)  ; е)
; е)  .
.
Задача 3.
1) Показать, что данные функции f и g являются бесконечно малыми или бесконечно большими при указанном стремлении аргумента.
2) Для каждой функции f и g записать главную часть (эквивалентную ей функцию) вида  при
при 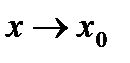 , или
, или  при
при  , указать их порядки малости (роста).
, указать их порядки малости (роста).
3) Сравнить f и g при  , если
, если  ,
, 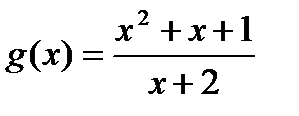 .
.
Задача 4. Найти точки разрыва функции  и определить их характер. Построить фрагменты графика функции в окрестности каждой точки разрыва:
и определить их характер. Построить фрагменты графика функции в окрестности каждой точки разрыва:

Рубежный контроль № 1
Срок проведения – 9-я неделя
Рубежный контроль по модулю № 1 включает в себя один теоретический вопрос, соответствующей программе 1-го модуля курса; одно задание, предполагающее запись определения предела функции по Коши, пять заданий на вычисление пределов и задание на поиск точек разрыва функции и исследование их характера.
Типовой вариант рубежного контроля № 1
1. Числовая последовательность. Предел последовательности; сходящиеся и расходящиеся последовательности. Доказать теорему о единственности предела сходящейся последовательности.
2. Сформулировать определение по Коши для предела 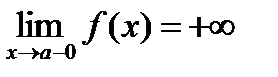 . Привести соответствующий пример (с геометрической иллюстрацией).
. Привести соответствующий пример (с геометрической иллюстрацией).
Вычислить пределы:
3.  . 4.
. 4. 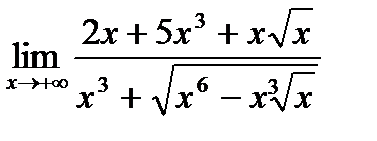 . 5.
. 5. 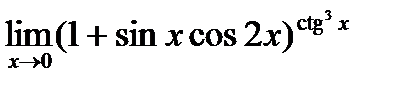 .
.
6. 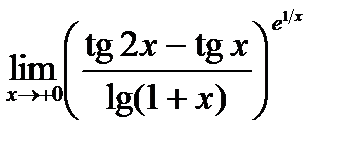 . 7.
. 7. 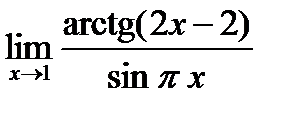 .
.
8. Найти точки разрыва функции 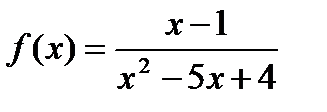 , исследовать их характер, построить график функции в их окрестности.
, исследовать их характер, построить график функции в их окрестности.
МОДУЛЬ 2. Дифференциальное исчисление фунуций одного переменного
Домашнее задание № 3 «Исследование функций и построение графиков»
Срок выдачи – 10-я неделя
Домашнее задание № 3 предполагает проведение полного исследования функции и построение графика трех заданных функций.
Срок сдачи – 15-я неделя.
Типовой вариант домашнего задания № 3
Исследовать заданные функции и построить их графики:
1) 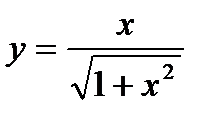 ; 2)
; 2) 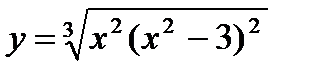 ; 3)
; 3) 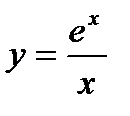 .
.
Контрольная работа «Техника дифференцирования»
Контрольная работа включает шесть заданий на вычисление производной функций, заданных явно, два задания на вычисление производных параметрически и неявно, а также задание на вывод уравнения касательной или нормали к кривой.
Срок проведения – 12-я неделя
Типовой вариант контрольной работы
Найти производную функции 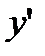 :
:
1. 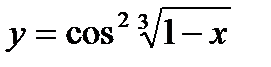 ; 2.
; 2. 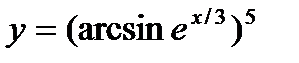 ; 3.
; 3. 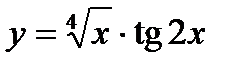 ;
;
4. 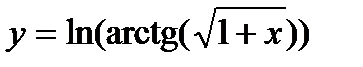 ; 5.
; 5. 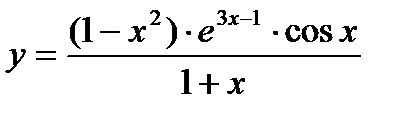 ; 6.
; 6. 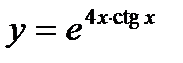 .
.
7. Найти 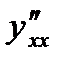 для функции, заданной параметрически:
для функции, заданной параметрически: 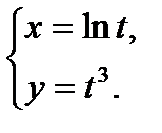
8. Найти 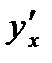 ,
, 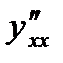 в точке
в точке 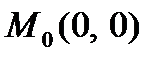 для функции, заданной неявно уравнением
для функции, заданной неявно уравнением
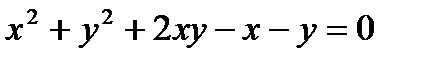
9. Найти уравнение касательной к эллипсу 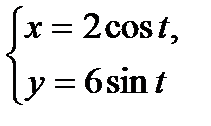 в точке
в точке 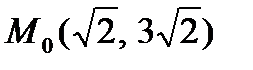 . Сделать чертеж.
. Сделать чертеж.
Рубежный контроль № 2
Срок проведения – 16-я неделя
Рубежный контроль по модулю № 2 включает в себя один теоретический вопрос, соответствующей программе 2-го модуля курса; одно задание, предполагающее проведение полного исследования функции и построение ее графика, и одно задание построить (схематично) график функции по заданному кусочно-линейному графику производной.
Типовой вариант контроля по модулю № 2
1. Доказать теорему Бернулли-Лопиталя для предела отношения двух бесконечно малых функций.
2. Исследовать функцию 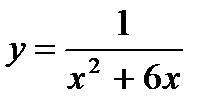 и построить ее график.
и построить ее график.
3. По графику производной построить график функции.
МОДУЛЬ 3. Итоговый экзамен
Срок проведения – экзаменационная сессия
Экзаменационный билет содержит два теоретических вопроса и две задачи, охватывающие оба модуля. Теоретические вопросы аналогичны тем, которые входят в программу подготовки к рубежному контролю по каждому из модулей.
Типовой вариант экзаменационного билета
1. Фундаментальные последовательности и их свойства. Доказать критерий Коши сходимости числовой последовательности.
2. Доказать необходимое условие возрастания (убывания) дифференцируемой функции.
3. Вычислить 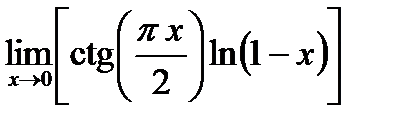 .
.
4. Построить график функции 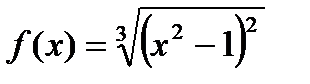 .
.
Вопросы для подготовки к контролю по модулям и к экзамену
Модуль 1. Элементарные функции и пределы
1. Принцип вложенных отрезков (Коши-Кантора).
2. Теорема о существовании точной верхней (нижней) грани ограниченного числового множества.
3. Теорема о единственности предела числовой последовательности.
4. Теорема об ограниченности сходящейся числовой последовательности.
5. Теорема Вейерштрасса о сходимости монотонной ограниченной последовательности.
6. Доказательство сходимости последовательности 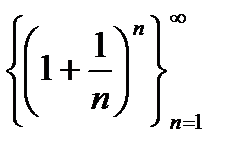
7. Предельная точка числового множества и ее свойства. Лемма о предельной точке (Больцано-Вейерштрасса).
8. Предельная точка числовой последовательности и ее свойства. Критерий сходимости числовой последовательности, связанный с существованием предельной точки.
9. Фундаментальные последовательности и их свойство. Критерий Коши сходимости числовой последовательности.
10. Предел функции. Теорема о связи двустороннего предела с односторонними.
11. Теорема о локальной ограниченности функции, имеющей конченый предел.
12. Бесконечно малые функции. Теорема о связи функции, ее предела и бесконечно малой.
13. Теоремы о сумме бесконечно малых и произведении б.м. на ограниченную функцию.
14. Теорема о пределе суммы, произведения, частного функций.
15. Теорема о пределе сложной функции.
16. Теорема о знакопостоянстве функции, имеющей отличный от нуля предел.
17. Теорема о предельном переходе в неравенстве.
18. Теорема о пределе промежуточной функции (теорема о 2-х милиционерах)
19. Теорема о связи бесконечно малой и бесконечно большой функции.
20. Первый замечательный предел 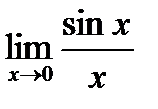 и следствия из него.
и следствия из него.
21. Второй замечательный предел 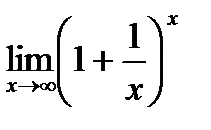 и следствия из него.
и следствия из него.
22. Теорема Вейерштрасса о пределе монотонной функции.
23. Теоремы об эквивалентных бесконечно малых.
24. Теоремы об эквивалентных бесконечно больших.
25. Непрерывность функции в точке. Свойства функций, непрерывных в точке. Непрерывность сложной функции.
26. Теоремы Больцано-Коши о нуле и о промежуточных значениях непрерывной на отрезке функции.
27. Теоремы Вейерштрасса об ограниченности непрерывной на отрезке функции и достижении этой функцией своих точных верхней и нижней граней.
28. Критерий инъективности непрерывной на отрезке функции. Теорема о точках разрыва монотонной функции.
29. Критерий непрерывности монотонной на отрезке функции. Теорема о непрерывности обратной функции.
30. Равномерная непрерывность. Теорема Кантора о равномерной непрерывности функции, непрерывной на отрезке.
Модуль 2. Дифференциальное исчисление функций одного переменного
1. Понятие производной. Геометрический смысл производной. Связь производной, секущей и касательной к графику функции.
2. Уравнения касательной и нормали к плоской кривой.
3. Дифференцируемость функции. Теорема о связи дифференцируемости функции с существованием конечной производной. Связь дифференцируемости и непрерывности функции.
4. Вычисление производных суммы, произведения и частного двух функций.
5. Теорема о дифференцируемости обратной функции.
6. Теорема о дифференцируемости сложной функции.
7. Вычисление производной функции, заданной параметрически, и заданной неявно.
8. Дифференциал функции. Геометрический смысл дифференциала. Теорема об инвариантности формы записи первого дифференциала.
9. Теорема Ферма. Необходимое условие экстремума дифференцируемой функции.
10. Теорема Ролля. Геометрический смысл теоремы Ролля.
11. Теорема Коши. Теорема Лагранжа. Геометрический смысл теоремы Лагранжа.
12. Теорема Бернулли-Лопиталя для предела отношения бесконечно малых функций.
13. Формула Тейлора с остаточным членом в форме Пеано.
14. Теорема о единственности разложения функции по формуле Тейлора с остаточным членом в форме Пеано.
15. Формула Тейлора с остаточным членом в общем виде, в форме Коши и Лагранжа.
16. Необходимое условие возрастания (убывания) дифференцируемой функции.
17. Достаточное условие возрастания (убывания) дифференцируемой функции.
18. Экстремумы функции. Достаточное условие экстремума по первой производной.
19. Достаточное условие экстремума по второй производной.
20. Достаточное условие экстремума по n -ой производной.
21. Выпуклость функции. Лемма о выпуклости функции.
22. Необходимое и достаточное условие выпуклости функции по первой производной.
23. Достаточное условие строгой выпуклости по второй производной.
24. Связь выпуклости дифференцируемой функции с положением касательной к графику функции.
25. Точки перегиба. Необходимое условие и достаточное условие существования точки перегиба.
26. Необходимое и достаточное условие существования наклонной асимптоты.
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Дисциплина состоит из 3-х учебных модулей и зачета.
Модуль 1
Таблица 7.1
| Виды аудиторных занятий и самостоятельной работы | Сроки проведения или выполнения,недели | Трудоёмкость,часы | Примечание |
| Упражнения | 1-6 | ||
| Домашние задания текущие | 1-6 | ||
| Рубежный контроль №1 |
Модуль 2
Таблица 7.2
| Виды аудиторных занятий и самостоятельной работы | Сроки проведения или выполнения,недели | Трудоёмкость,часы | Примечание |
| Упражнения | 7-17 | ||
| Домашние задания текущие | 7-17 | ||
| Рубежный контроль №2 |
Модуль 1
Лекции
Векторная алгебра
Лекция 1. Скалярные и векторные величины. Понятие геометрического вектора (направленного отрезка). Нуль-вектор, единичный вектор (орт). Коллинеарные и компланарные векторы. Равенство векторов. Связанные, скользящие, свободные векторы. Линейные операции над векторами, свойства этих операций. Ортогональная проекция векторов на направление. Теоремы о проекциях (доказать самостоятельно).
ОЛ-1, пп. 1.1–1.4; ОЛ-3, гл.2 §1, гл.1 §2 п.1.
Лекция 2. Линейная комбинация векторов. Линейная зависимость векторов. Критерий линейной зависимости двух и трех векторов, линейная зависимость четырех векторов (доказать самостоятельно). Векторные пространства V1, V2, V3 и базисы в них. Разложение вектора по базису. Координаты вектора. Линейные операции над векторами, заданными своими координатами. Ортонормированный базис. Скалярное произведение векторов, его механический смысл. Вычисление скалярного произведения векторов, заданных своими координатами в ортонормированном базисе. Вычисление длины вектора, косинуса угла между векторами и проекции вектора на направление. Координаты вектора в ортонормированном базисе как проекции этого вектора на направление базисных векторов. Направляющие косинусы вектора.
ОЛ-1, пп. 1.5–1.7, 2.2; ОЛ-3, гл. 2, §§1–2, гл. 1, §1, п. 3.
Лекция 3. Ориентация базиса, правые и левые тройки векторов. Векторное произведение двух векторов, его механический и геометрический смысл. Свойства векторного произведения (без док-ва). Вычисление векторного произведения в координатной форме в ортонормированном базисе. Смешанное произведение трех векторов и его геометрический смысл. Объем тетраэдра. Свойства смешанного произведения. Вычисление смешанного произведения в ортонормированном базисе. Условие компланарности трех векторов.
ОЛ-1, пп. 2.3–2.5; ОЛ-3, гл. 2, §3.
Прямые и плоскости
Лекция 4. Декартова прямоугольная система координат на плоскости и в пространстве. Радиус-вектор точки, координаты точки; связь координат вектора с координатами его начала и конца. Простейшие задачи аналитической геометрии: вычисление длины отрезка, деление отрезка в данном отношении. Геометрический смысл уравнения 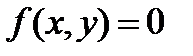 на плоскости и
на плоскости и 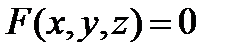 в пространстве. Различные виды уравнения прямой на плоскости: общее уравнение, параметрические уравнения, каноническое уравнение, уравнение прямой с угловым коэффициентом, уравнение прямой “в отрезках”. Нормальный и направляющий векторы прямой. Взаимное расположение двух прямых на плоскости. Вычисление угла между прямыми.
в пространстве. Различные виды уравнения прямой на плоскости: общее уравнение, параметрические уравнения, каноническое уравнение, уравнение прямой с угловым коэффициентом, уравнение прямой “в отрезках”. Нормальный и направляющий векторы прямой. Взаимное расположение двух прямых на плоскости. Вычисление угла между прямыми.
ОЛ-1, пп. 3.1–3.5, 4.1–4.3; ОЛ-3, гл. 2, §1 п. 9, гл. 4 §1, гл. 5, §1.
Лекция 5. Нормальное уравнение прямой. Расстояние от точки до прямой. Различные виды уравнения плоскости в пространстве: общее уравнение плоскости; уравнение плоскости, проходящей через три точки; уравнение плоскости “в отрезках”. *Связка плоскостей. Взаимное расположение двух плоскостей в пространстве. Угол между плоскостями. Нормальное уравнение плоскости Расстояние от точки до плоскости.
ОЛ-1, пп. 4.4, 5.1; ОЛ-3, гл. 5, §1, п. 7, §3.
Лекция 6. Прямая в пространстве. Общие уравнения прямой. Параметрические уравнения прямой; векторное уравнение прямой; канонические уравнения прямой. Уравнения прямой, проходящей через две заданные точки. Взаимное расположение прямой и плоскости, угол между прямой и плоскостью. Взаимное расположение двух прямых в пространстве, угол между прямыми в пространстве. Расстояние от точки до прямой в пространстве. Расстояние между двумя прямыми.
ОЛ-1, пп. 5.3–5.5; ОЛ-3, гл. 5, §4.
.
Упражнения
Векторная алгебра
Занятия 1-2. Определители и их свойства. Решение систем линейных уравнений по формулам Крамера.
Ауд.: изложение теории;
ОЛ-2 №№ 3.2, 3.8, 3.13, 3.19, 3.22, 3.25, 3.27, 3.51, 3.53, 3.187, 3.189, 3.191, 3.198 или
ДЛ-2 №№ 1204(8), 1205(3), 1206(1), 1211, 1213, 1217, 1219, 1221, 1223, 1224, 1234(2), 1252, 1237, 1239, 1240, 1242, 1247.
Дома: ОЛ-2 №№ 3.3 9, 3.12, 3.20, 3.21, 3.28, 3.50, 3.52, 3.188, 3.190, 3.192, 3.199 или
ДЛ-2 №№ 1204(7), 1205(4), 1206(2), 1212, 1214, 1218, 1220, 1225, 1235(2), 1253, 1238, 1241, 1243, 1251.
Занятие 3. Линейные операции с векторами. Разложение вектора по базису.
Ауд.: ОЛ-2 №№ 2.7 2.8, 2.19, 2.20, 2.38, 2.39, 2.44, 2.46, 2.51, 2.56, 2.57 или
ДЛ-2 №№ 769(1,3), 773(1,3,5), 775(2,4,6), 777, 779, 783, 788, 789, 794, 771.
Дома: ОЛ-2 №№ 2.10, 2.22, 2.36, 2.37, 2.45, 2.46, 2.52, 2.58 или
ДЛ-2 №№ 769(2,4), 773(2,4), 775(1,3,5), 776, 778, 785, 787, 793.
Занятие 4. Скалярное произведение векторов и его приложения.
Ауд.: ОЛ-2 №№ 2.40, 2.65, 2.70, 2.78(б, г, ж, з, и), 2.80, 2.82, 2.84, 2.89 или
ДЛ-2 №№ 795(1,3,5,7), 808, 814(1,4), 815, 818, 821, 826, 833, 780, 825.
Дома: ОЛ-2 №№ 2.66, 2.67, 2.71, 2.72, 2.78(а, в, д), 2.81, 2.83, 2.88 или
ДЛ-2 №№ 795(2,4,6), 812(1,4,5), 820, 824, 830, 835, 781, 813, 817, 819.
Занятие 5. Векторное произведение векторов и его приложения.
Ауд.: ОЛ-2 №№ 2.98(а, б), 2.99, 2.100(а, б), 2.108, 2.109, 2.115, 2.118, 2.120 или
ДЛ-2 №№ 839, 843, 844, 850, 854, 855, 857, 840, 861, 862.
Дома: ОЛ-2 №№ 2.98(в), 2.100(в, г), 2.105, 2.106(в), 2.107, 2.111, 2.116, 2.119 или
ДЛ-2 №№ 841, 842, 848, 851, 858, 859, 853, 860.
Занятие 6. Смешанное произведение векторов и его приложения.
Ауд.: ОЛ-2 №№ 2.125, 2.127(а), 2.129, 2.130, 2.132, 2.134, 2.135(а), 2.136(а), 2.137, 2.138(а), 2.140(а, в) или
ДЛ-2 №№ 865(1,3,5), 867, 868, 869, 871, 874(1,2), 875, 877, 878.
Дома: ОЛ-2 №№ 2.124, 2.126, 2.127(б), 2.133, 2.135(б), 2.136(б), 2.138(б), 2.139, 2.140(б, г) или
ДЛ-2 №№ 865(2,4,6), 866, 870, 873, 874(3), 876.
Прямые и плоскости
Занятие 7. Плоскость в пространстве.
Ауд.: ОЛ-2 №№ 2.180(а), 2.181(а), 2.182(а), 2.183(а), 2.184(б), 2.185, 2.190, 2.196, 2.191 или
ДЛ-2 №№ 916, 917, 921, 930, 932, 926(1), 927(1), 940(1), 941(3), 942(2), 947, 949, 964(1).
Дома: ОЛ-2 №№ 2.180(б), 2.181(б), 2.192(б), 2.193(б), 2.194(а), 2.187, 2.188, 2.189, 2.195 или
ДЛ-2 №№ 914, 991, 929, 931, 934, 926(2), 927(2), 940(2), 941(1), 942(3), 950, 964(2).
Занятия 8. Прямая в пространстве. Взаимное расположение прямых и плоскостей в пространстве.
Ауд.: ОЛ-2 №№ 2.197(а), 2.198, 2.200(а), 2.204, 2.205(а), 2.208, 2.214 или
ДЛ-2 №№ 1010(1), 1007, 1018, 1020(1), 1023, 1042, 1050, 1063(1), 991, 1052.
Дома: ОЛ-2 №№ 2.197(б), 2.199, 2.201, 2.203(б), 2.205(б), 2.206, 2.210, 2.215 или
ДЛ-2 №№ 1008(1), 1009(1), 1024, 1043, 1054, 1063(2), 993
Занятия 9. Контроль по модулю №1 (РК №1)






