ЛИТЕРАТУРА
Основная литература (ОЛ)
1. Морозова В.Д. Введение в анализ. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2005. – 408 с.
2. Иванова Е.Е. Дифференциальное исчисление функций одного аргумента. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2001. – 408 с.
3. Задачи и упражнения по математическому анализу для втузов / Под ред. Б.П. Демидовича. – М.: Астрель, 2003. – 472 с.
Дополнительная литература (ДЛ)
1. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. Т. 1. – М.: Интеграл-Пресс, 2006. – 416 с.
2. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т. 1. – М.: ФИЗМАТЛИТ, 2003. – 680 с.
3. Сборник задач по математике для втузов. Ч. 1. Линейная алгебра и основы математического анализа: Учеб. пособие для втузов / Под ред. А.В. Ефимова, Б.П. Демидовича. – М.: Наука, 1993. – 478 с.
4. Ильин В.А., Позняк Э.Г. Основы математического анализа. Ч.1. – М.: Наука, 1982. – 616 с.
5. Кудрявцев Л.Д. Курс математического анализа. Т. 1. – М.: Высш. школа, 1988. – 718 с.
6. Вся высшая математика: Учебник для втузов / М.Л. Краснов, А.И. Киселев, Г.И. Макаренко и др. Т. 1. – М.: Эдиториал УРСС, 2000. – 328 с.
7. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. – М.: Наука, 1988. – 431 с.
Методические и учебные пособия (МП)
1. Галкин С.В. Математический анализ. Методические указания по материалам лекций для подготовки к экзамену в первом семестре. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2004. – 116 с.
2. Грибов А.Ф., Котович А.В., Минеева О.М. Кривые на плоскости, заданные параметрически и в полярной системе координат. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2004.
3. Казанджан Э.П. Исследование функций и построение графиков. – М.: Изд-во МГТУ им. Н.Э. Баумана, 1995.
4. Ильичев А.Т., Кузнецов В.В., Фаликова И.Д. Графики элементарных функций. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2004.
5. Соболев С. К., Ильичев А.Т. Исследование и построение плоских кривых, заданных параметрически и в полярных координатах. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2004. – 80 с.
6. Казанджан Э.П., Казанджан Г.П. Вычисление пределов. – М.: Изд-во МГТУ им. Н.Э. Баумана, 1995.
7. Введение в анализ / Под ред. Е.Е. Ивановой. – М.: МГТУ, 1990. – 85с.
8. Казанджан Г.П., Казанджан Э.П. Рабочий справочник по математике. – М.: МГТУ, 2002.
9. Михайлова Т.Ю., Поляшова Р.Г., Титов К.В. Исследование свойств функций и построение графиков. Формула Тейлора и ее приложения. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2002.
10. Казанджан Э.П. Графики. Сборник задач с примерами решений по исследованию функций и построению графиков. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2004.
11. Дуров В.В., Мастихин А.В., Савин А.С. Пределы и непрерывность функций. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2004. – 62 с.
ЛЕКЦИИ
Модуль 1. Элементарные функции и пределы
Лекция 1-2. Введение в курс. Элементы логики. Высказывания и предикаты, операции над ними. Кванторы. Построение отрицания сложного высказывания. Теорема как импликация. Необходимость и достаточность. Прямая, обратная и противоположная теоремы, связь между ними. Доказательство от противного. Метод математической индукции. Неравенство Бернулли. Бином Ньютона. Множества, операции над ними, их свойства. Множество R действительных чисел и его аксиоматика. Полнота множества R. Промежутки. Окрестности конечной точки и бесконечности. Принцип вложенных отрезков (Коши-Кантора). Ограниченные и неограниченные множества в R. Точные верхняя и нижняя грани множества. Принцип Архимеда и следствия из него.
ОЛ-1 гл. 1;
ДЛ-2 Введение.
Лекция 3. Отображение и функция. График функции. Виды отображений: сюръективное, инъективное, биективное. Обратное отображение. Понятие мощности множества. Счетные множества. Несчетность множества R. Композиция функций. Числовые функции одного действительного переменного и их свойства: ограниченность, монотонность, четность, периодичность. Основные элементарные функции и их свойства.
ОЛ-1 гл. 2, 3;
ДЛ-1 гл. I §§ 6–9;
ДЛ-2 гл. 2 § 1.
Лекция 4. Числовая последовательность, ее ограниченность и монотонность. Предел последовательности. Бесконечно малая и бесконечно большая последовательности. Свойства сходящихся последовательностей. Теорема Вейерштрасса.
ОЛ-1 пп. 6.1–6.5, 6.7;
ДЛ-2 гл. 1 § 1, § 3 (п. 34, 35).
Лекции 5. Теорема об арифметических операциях под знаком предела. Число е как предел числовой последовательности. Гиперболические функции. Предельные точки множества. Принцип Больцано-Вейерштраса. Предельные точки последовательности. Фундаментальная числовая последовательность. Критерий Коши сходимости числовой последовательности.
ОЛ-1 пп. 6.6, д.6.1, д.6.2.;
ДЛ-2 гл. 1 § 2 (п. 30), § 3 (п. 36, 37), § 4.
Лекция 6. Определение предела функции по Коши. Теорема о связи двустороннего предела с односторонними. Определение предела функции по Гейне. Эквивалентность определений предела по Гейне и Коши (без доказательства). Теорема о единственности предела функции. Теорема о локальной ограниченности функции, имеющей конечный предел.
ОЛ-1 пп. 7.1–7.4;
ДЛ-1 гл. II, §§ 2–3;
ДЛ-2 гл. 2 § 2 (п. 52–56).
Лекция 7. Бесконечно малые функции. Теорема о связи функции, ее предела и бесконечно малой. Свойства бесконечно малых функций. Теорема об арифметических операциях над функциями, имеющими предел. Теорема о пределе сложной функции (замена переменной в пределе). Теорема о знакопостоянстве функции, имеющей отличный от нуля предел. Предельный переход в неравенстве. Теорема о пределе промежуточной функции (теорема «о двух милиционерах»).
ОЛ-1 пп. 7.5–7.6;
ДЛ-1 гл. II §§ 4–5;
ДЛ-2 гл. 2 § 2 (п. 55–56).
Лекция 8. Бесконечно большие функции. Теорема о связи бесконечно больших и бесконечно малых функций. Первый замечательный предел и следствия из него. Второй замечательный предел и следствия из него. Теорема Вейерштрасса о пределе монотонной и ограниченной функции.
ОЛ-1 пп. 7.5, 7.7, 7.8;
ДЛ-1 гл. II §§ 6–7;
ДЛ-2 гл. 2 § 3 (п. 65), гл. 2 § 2 (п. 54–57).
Лекция 9. Сравнение бесконечно малых. Порядок малости, эквивалентные бесконечно малые, несравнимые бесконечно малые. Таблица эквивалентных бесконечно малых. Свойства эквивалентных бесконечно малых. Правила работы с «о малое». Сравнение бесконечно больших. Теоремы об эквивалентных бесконечно больших.
ОЛ-1 гл. 10;
ДЛ-1 гл. II § 11;
ДЛ-2 гл. 2 § 3 (п. 60–64).
Лекция 10. Непрерывность функции в точке. Различные определения непрерывности и их эквивалентность. Приращение аргумента, приращение функции. Непрерывность функции в интервале. Односторонняя непрерывность в точке. Непрерывность функции на отрезке. Свойства функций, непрерывных в точке (связь непрерывности с односторонней непрерывностью, локальная ограниченность, знакопостоянство, арифметические операции с непрерывными функциями, предельный переход, непрерывность сложной функции). Точки разрыва и их классификация.
ОЛ-1 пп. 9.1–9.3;
ДЛ-1 гл. II §§ 9–10;
ДЛ-2 гл. 2 § 4 (п. 66–70).
Лекция 11. Свойства функций, непрерывных на отрезке (теоремы о нулях, о промежуточных значениях, об ограниченности, о достижении точных граней непрерывной на отрезке функции). Непрерывность на отрезке монотонной функции, связь непрерывности, инъективности и строгой монотонности. Теорема о существовании обратной функции. Точки разрыва монотонной функции. Критерий непрерывности монотонной функции. Теорема о непрерывности обратной функции.
ОЛ-1 пп. 9.4–9.5, д.9.1, д.9.2;
ДЛ-2 гл. 2 § 5 (п. 80–85), § 4 (п. 71).
Лекция 12. Непрерывность основных элементарных функций (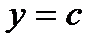
, 
, 
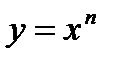, многочлен, дробно-рациональная функция, 
, 
, 
, 
, 
, 
, 
, 
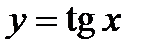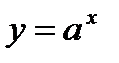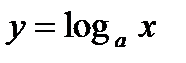). Равномерная непрерывность функций. Связь между равномерной непрерывностью на множестве и непрерывностью в точке этого множестве. Теорема Кантора о равномерной непрерывности функции на отрезке.
ОЛ-1 пп. 9.5, 5.9;
ДЛ-2 гл. 2 § 5 (п. 86–87), § 4 (п. 72–73).
Модуль 2. Дифференциальное исчисление функций одного переменного
Лекции 13. Производная функции в точке. Бесконечная производная. Примеры вычисления производной. Геометрический смысл производной. Связь существования наклонной касательной к графику и наличия конечной производной функции в точке. Левая и правая производные; левая и правая наклонные касательные. Нормаль к графику функции. Дифференцируемость функции в точке. Теоремы о связи дифференцируемости с существованием конечной производной и с непрерывностью. Основные правила дифференцируемости (производные сумы, разности, произведения, частного).
ОЛ-2 гл. 1, п. 2.1;
ДЛ-1 гл. III §§ 1–4, § 7;
ДЛ-2 гл. 3 § 1 (п. 90–93, 96–97, 100–101), § 2 (п. 103–104).
Лекции 14. Теоремы о дифференцируемости обратной и сложной функций. Производные основных элементарных функций. Логарифмическая производная и производная показательно-степенной функции. Производные функций, заданных параметрически и неявно. Производные высших порядков. Вычисление производных высших порядков для функций 
, 
, 
, 
, 
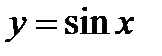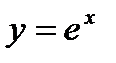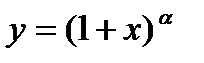. Формула Лейбница для вычисления производной произведения.
ОЛ-2 пп. 2.2–2.6; 4.1–4.4;
ДЛ-1 гл. III §§ 5–6, §§ 8–15, §§ 18–19, § 22;
ДЛ-2 гл. 3 § 1 (п. 94–95, 98–99), § 4 (п. 115–118).
Лекции 15. Дифференциал функции. Теорема о связи производной и дифференциала. Геометрический смысл дифференциала. Правила работы с дифференциалами (дифференциал суммы, разности, произведения, частного). Инвариантность формы записи первого дифференциала. Приближенные вычисления с помощью дифференциалов. Дифференциалы высших порядков, отсутствие инвариантности.
ОЛ-2 гл. 3, п. 4.5;
ДЛ-1 гл. III §§ 20–21, § 23;
ДЛ-2 гл. 3 § 2, § 4 (п. 119-120).
Лекции 16. Основные теоремы дифференциального исчисления (Ферма, Ролля, Коши, Лагранжа) и их геометрический смысл. Теорема Бернулли-Лопиталя и раскрытие неопределенности типа [0/0]. Теорема Бернулли-Лопиталя и раскрытие неопределенности типа [ 
/ 
] (без доказательства). Сравнение порядков роста логарифмической, степенной и показательной функций на бесконечности. Раскрытие неопределенностей типа [ 
], [ 
], [ 
], [ 
], [ 
].
ОЛ-2 гл. 5, гл. 6;
ДЛ-1 гл. IV §§ 1–5;
ДЛ-2 гл. 3 § 3, гл. 4 § 4.
Лекция 17. Формула Тейлора для многочленов. Многочлен Тейлора для произвольных функций. Формула Тейлора с остаточным членом в форме Пеано. Теорема о единственности разложения функции по формуле Тейлора с остаточным членом в форме Пеано. Формула Тейлора с остаточным членом в общем виде. Следствия: остаточный член в форме Коши и в форме Лагранжа. Формула Маклорена.
ОЛ-2 пп. 7.1–7.3;
ДЛ-1 гл. IV § 6;
ДЛ-2 гл. 3 § 5 (п. 123, 124, 126).
Лекция 18. Разложение элементарных функций по формуле Маклорена (
, 
, 
, 
, 
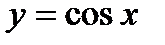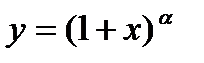). Использование разложений для вычисления пределов и в приближенных вычислениях. Применение дифференциального исчисления для исследования функций и построения их графиков. Связь производной и монотонности. Необходимые и достаточные условия монотонности. Локальный экстремум функции. Необходимое условие локального экстремума дифференцируемой функции.
ОЛ-2 пп. 7.4, 7.5, д.7.1, 8.1, 8.2;
ДЛ-1 гл. IV § 7, гл. V §§ 2–3;
ДЛ-2 гл. 3 § 5 (п. 125, 127), гл. 4 § 1 (п. 131, 132, 134).
Лекция 19. Достаточные условия существования экстремума по первой производной, по второй производной, по n -ой производной. Понятие о выпуклости вверх (вниз) функции. Геометрический смысл определения выпуклости функции – взаимное расположение графика функции и хорды. Лемма о выпуклости функции и ее геометрический смысл.
ОЛ-2 пп.8.3, 8.4;
ДЛ-1 гл. V §§ 3–5, 8–9;
ДЛ-2 гл. 4 § 1 (п. 135–138), § 2 (п. 141–143).
Лекция 20. Необходимое и достаточное условие выпуклости по первой производной. Необходимое и достаточное условие выпуклости дважды дифференцируемой функции, достаточное условие строгой выпуклости дважды дифференцируемой функции. Связь направления выпуклости графика функции с положением касательной. Точки перегиба графика функции. Необходимое и достаточное условия существования точки перегиба. Асимптоты графика функции: вертикальные, горизонтальные, наклонные. Теорема о наклонной асимптоте. Общая схема исследования функций и построения их графиков.
ОЛ-2 пп.8.4, 8.5, 8.7, 8.8;
ДЛ-1 гл. V §§ 9–11;
ДЛ-2 гл. 4 § 2 (п. 143, 145), § 2.
Лекции 21. Векторная функция скалярного аргумента. Геометрическая интерпретация. Годограф вектор-функции. Способы задания кривой в пространстве: векторное уравнение, параметрическое уравнение, пересечение двух поверхностей. Предел вектор-функции и его связь с пределами координатных функций. Правила вычисления пределов вектор-функций. Непрерывность вектор-функции. Теорема о связи непрерывности вектор-функции и непрерывности координатных функций (без доказательства).
ОЛ-2 п. 9.1;
ДЛ-1 гл IX, §§ 1–2.
Лекция 22. Производная вектор-функции скалярного аргумента. Теорема о связи производной вектор-функции и производных координатных функций. Геометрический смысл производной вектор-функции. Правила вычисления производных. Дифференцируемость вектор-функции. Связь дифференцируемости и наличия конечной производной. Дифференциал вектор-функции.
ОЛ-2 п. 9.2;
ДЛ-1 гл IX, §§ 2–3.
Лекция 23. Простейшие численные методы решения уравнений вида 
. Нули многочленов и точные решения алгебраических уравнений. Локализация и уточнение корней. Деление отрезка пополам, введение в итерационные методы, метод Ньютона.
ОЛ-2 гл.11;
Лекция 24. Обзорная. Резерв.
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
Модуль 1. Элементарные функции и пределы
Занятия 1–3. Основные элементарные функции их свойства и графики. Кривые в полярных координатах.
Ауд.: ОЛ-3 №№ 63, 67, 71, 72, 77, 91, 93, 101, 102, 110, 116, 118, 128 (а), 132, 135, 136, 139, 140, 146, 153; раздаточный материал.
Дома: ОЛ-3 №№ 51 (2), 60, 65, 69, 73, 92, 95, 112, 114, 122, 127 (а), 136, 138, 141, 145, 154.
Занятия 4–5. Операции над множествами, их свойства. Элементы логики. Метод математической индукции.
Ауд. и Дома: ДЛ-3 №№ 1.28–1.71, 1.83–1.94, МП-7.
Занятие 6. Пределы числовых последовательностей. Пределы функций.
Ауд.: ОЛ-3 №№ 166 (а), 171, 175, 177, 179, 181, 184, 186, 188, 211, 213, 215, 183.
Дома: ОЛ-3 №№ 167 (а), 172, 173, 176, 180, 182, 185, 187, 190, 214, 212 или
Ауд.: ДЛ-3 №№ 1.230 (б), 1.232, 1.233, 1.235, 1.236, 1.238, 1.240, 1.282, 1.284, 1.299, 1.301.
Дома: ДЛ-3 №№ 1.230 (г), 1.234, 1.239, 1.241, 1.243, 1.283, 1.286, 1.294, 1.299, 1.300, 1.302, 1.237.
Занятие 7. Пределы функций. Первый замечательный предел.
Ауд.: ОЛ-3 №№ 191, 193, 195, 198, 200, 202, 203, 206, 197, 209, 216, 218, 220, 223, 224, 233, 236, 240.
Дома: ОЛ-3 №№ 192, 194, 196, 199, 201, 205, 204, 207, 210, 219, 222, 226, 231, 235, 238, 229 или
Ауд.: ДЛ-3 №№ 1.272, 1.274, 1.277, 1.285, 1.289, 1.292, 1.298, 1.304, 1.306, 1.308, 1.310, 1.312, 1.314, 1.316, 1.293.
Дома: ДЛ-3 №№ 1.273, 1.275, 1.276, 1.281, 1.288, 1.290, 1.291, 1.297, 1.303, 1.305, 1.307, 1.309, 1.311, 1.313, 1.315.
Занятие 8. Пределы функций. Второй замечательный предел. Односторонние пределы.
Ауд.: ОЛ-3 №№ 241, 243, 245, 247, 249, 251, 252, 253, 254, 259, 261, 263, 264, 266, 268, 270.
Дома: ОЛ-3 №№ 242, 244, 246, 248, 250, 255, 256, 257, 258, 260, 262, 265, 267, 269 или
Ауд.: ДЛ-3 №№ 1.320, 1.322, 1.324, 1.317, 1.318, 1.326, 1.328, 1.330, 1.332, 1.335, 1.337, 1.338, 1.341, 1.342, 1.345.
Дома: ДЛ-3 №№ 1.321, 1.323, 1.325, 1.327, 1.329, 1.331, 1.333, 1.336, 1.339, 1.340, 1.343, 1.344, 1.346.
Занятие 9. Сравнение бесконечно малых и бесконечно больших. Вычисление пределов функций и приближенных значений функций с помощью эквивалентных бесконечно малых.
Ауд.: ОЛ-3 №№ 289 (б), 290 (б), 292, 293 (а,в,г), 295, 296, 297, 298, 300 (а,г), 301 (а(1,3), в(6)), 302, 303 (б,в).
Дома: ОЛ-3 №№ 288 (а), 290 (в), 291, 293 (б,д), 294, 299, 300 (б,в), 301 (б(4), г(7)), 303 (а,г) или
Ауд.: ДЛ-3 №№ 1.349, 1.351, 1.353, 1.355, 1.357, 1.359 (а,в), 1.360, 1.362, 1.366, 1.368, 1.370, 1.372, 1.374, 1.376.
Дома: ДЛ-3 №№ 1.350, 1.352, 1.354, 1.356, 1.358, 1.359 (б), 1.363, 1.367, 1.361, 1.369, 1.371, 1.373, 1.375, 1.377.
Занятия 10–11. Непрерывность функций. Точки разрыва и их классификация.
Ауд.: ОЛ-3 №№ 309, 310 (а) 313, 315, 316 (а,в,д), 317, 319, 321, 323, 326, 329, 330.
Дома: ОЛ-3 №№ 307, 310 (б), 314, 316 (б,г,е), 318, 322, 324, 325, 327, 328 или
Ауд.: ДЛ-3 №№ 1.381, 1.384, 1.386, 1.388, 1.390, 1.392, 1.394, 1.395, 1.397, 1.399, 1.401, 1.402.
Дома: ДЛ-3 №№ 1.382, 385, 1.387, 1.391, 1.393, 1.396, 1.398, 1.400, 1.403, 1.389.
Занятие 12. Контроль по модулю № 1.
Модуль 2. Дифференциальное исчисление функций одного переменного
Занятие 13. Дифференцирование. Правила дифференцирования.
Ауд.: ОЛ-3 №№ 358 (а,г), 368, 377, 379, 383, 385, 389, 390, 396, 398, 402, 403, 414, 427, 430, 445, 447, 453.
Дома: ОЛ-3 №№ 358 (б,в), 393, 369, 375, 378, 384, 386, 387, 388, 394, 399, 401, 404, 415, 425, 429, 442, 446, 452 или
Ауд.: ДЛ-3 №№ 5.6, 5.11, 5.21, 5.23, 5.25, 5.27, 5.29, 5.31, 5.35, 5.45, 5.49, 5.37, 5.39, 5.48, 5.51, 5.53, 5.55, 5.57, 5.41.
Дома: ДЛ-3 №№ 5.3, 5.7, 5.10, 5.12, 5.22, 5.26, 5.28, 5.32, 5.34, 5.46, 5.50, 5.38, 5.40, 5.44, 5.47, 5.52, 5.54, 5.56, 5.42.
Занятие 14. Дифференцирование. Дифференцирование сложной функции и функции, заданной параметрически.
Ауд.: ОЛ-3 №№ 461, 464, 474, 476, 479, 495, 530, 497, 501, 507, 513, 526, 533, 537, 553, 554 (б,в,г), 582, 593, 594, 596.
Дома: ОЛ-3 №№ 463, 475, 481, 485, 494, 496, 500, 504, 508, 512, 516, 520, 539, 523, 531, 534, 540, 552, 554 (а,д), 586, 589, 592, 597 или
Ауд.: ДЛ-3 №№ 5.59, 5.61, 5.73, 5.63, 5.66, 5.67, 5.75, 5.76, 5.93, 5.95, 5.101, 5.105, 5.108, 5.168, 5.171, 5.173, 5.175, 5.177, 5.179, 5.180.
Дома: ДЛ-3 №№ 5.58, 5.60, 5.62, 5.70, 5.64, 5.65, 5.68, 5.71, 5.73, 5.74, 5.94, 5.100, 5.102, 5.106, 5.169, 5.172, 5.176, 5.178, 5.182, 5.196.
Занятие 15. Дифференцирование. Логарифмическая производная. Производная функции, заданной неявно. Производные высших порядков.
Ауд.: ОЛ-3 №№ 567, 571, 573, 575, 579, 577, 605, 609, 611, 613, 615, 617, 620 (б), 669, 670, 676, 689 (а,в,д), 692, 697, 707, 709.
Дома: ОЛ-3 №№ 568, 570, 572, 576, 578, 580, 604, 608, 612, 614, 620 (в), 689 (б,г,е), 694, 695, 701, 708, 711 (б), 574 или
Ауд.: ДЛ-3 №№ 5.81, 5.83, 5.85, 5.87, 5.89, 5.92, 5.111, 5.144, 5.146, 5.148, 5.150, 5.152, 5.154, 5.156, 5.186, 5.188, 5.201, 5.202, 5.224, 5.225, 5.230, 5.232, 5.233.
Дома: ДЛ-3 №№ 5.82, 5.84, 5.86, 5.88, 5.91, 5.110, 5.112, 5.145, 5.147, 5.149, 5.151, 5.153, 5.155, 5.184, 5.187, 5.189, 5.200, 5.203, 5.223, 5.226, 5.231, 5.234, 5.90.
Занятие 16. Дифференцирование. Геометрический смысл производной и дифференциала. Применение дифференциала к приближенным вычислениям значений функций.
Ауд.: ОЛ-3 №№ 633 (а,в,г), 634, 636, 626, 644, 646, 712, 719, 722, 723, 724, 725, 734, 737 (а,в,г), 741 (б,в), 743, 726.
Дома: ОЛ-3 №№ 633 (б,д), 635, 636, 637, 639, 643, 645, 713, 720, 721, 727, 728, 730, 730, 732, 735, 737 (б,д), 741 (а,в), 744 или
Ауд.: ДЛ-3 №№ 5.235, 5.238, 5.240, 5.241, 5.243, 5.246, 5.256, 5.277, 5.281 (б), 5.285, 5.287, 5.288, 5.290, 5.292, 5.294, 5.297, 5.298 (а,в), 5.300.
Дома: ДЛ-3 №№ 5.236, 5.237, 5.238, 5.242, 5.244, 5.245, 5.249, 5.250, 5.255 (а), 5.286, 5.289, 5.291, 5.295, 5.296, 5.298 (б), 5.299.
Занятие 17. Контрольная работа “Техника дифференцирования”.
Занятие 18. Правило Бернулли-Лопиталя раскрытия неопределенностей.
Ауд.: ОЛ-3 №№ 777, 778, 779, 781, 784, 788, 792, 793, 795, 797, 799, 800, 803, 804, 806, 809.
Дома: ОЛ-3 №№ 780, 782, 783, 785, 789, 791, 794, 796, 801, 805, 807, 808 или
Ауд.: ДЛ-3 №№ 5.329, 5.330, 5.332, 5.334, 5.336, 5.340, 5.342, 5.344, 5.347, 5.348, 5.352, 5.354, 5.353, 5.358, 5.360, 5.363, 5.365, 5.366, 5.369, 5.371, 5.373, 5.378.
Дома: ДЛ-3 №№ 5.331, 5.333, 5.335, 5.337, 5.341, 5.343, 5.345, 5.346, 5.349, 5.351, 5.355, 5.356, 5.359, 5.361, 5.362, 5.364, 5.367, 5.370, 5.372, 5.376.
Занятие 19. Формула Тейлора.
Ауд.: ОЛ-3 №№ 768, 769, 772 (а), 774, 775.
Дома: ОЛ-3 №№ 770, 771, 772 (б), 773 или
Ауд.: ДЛ-3 №№ 5.383, 5.385, 5.389, 5.391, 5.392, 5.394, 5.395, 5.397 (а,в), 5.400 (а,б).
Дома: ДЛ-3 №№ 5.382, 5.386, 5.388, 5.390, 5.393, 5.396, 5.397 (б,г), 5.398 (б), 5.400 (в).
Занятие 20. Исследование функций. Асимптоты графиков функций, интервалы возрастания, убывания, экстремумы.
Ауд.: ОЛ-3 №№ 903, 907, 911, 913, 818, 825, 833.
Дома: ОЛ-3 №№ 904, 906, 908, 910, 815, 819, 821 или
Ауд.: ДЛ-3 №№ 5.454, 5.455, 5.456, 5.406, 5.404, 5.410.
Дома: ДЛ-3 №№ 5.452, 5.453, 5.457, 5.458, 5.405, 5.408, 5.409
Занятие 21. Исследование функций и построение их графиков.
Ауд.: ОЛ-3 №№ 898, 900, 921, 938.
Дома: ОЛ-3 №№ 895, 899, 931, 933 или
Ауд.: ДЛ-3 №№ 5.444, 5.446, 5.466, 5.496.
Дома: ДЛ-3 №№ 5.442, 5.445, 5.472, 5.497.
Занятие 22. Исследование функций и построение их графиков.
Ауд.: ОЛ-3 №№ 943, 953, 973, 989.
Дома: ОЛ-3 №№ 945, 946, 974, 988 или
Ауд.: ДЛ-3 №№ 5.493, 5.500, 5.516, 5.525.
Дома: ДЛ-3 №№ 5.494, 5.502, 5.517, 5.526
Занятие 23. Практические задачи на наибольшие и наименьшие значения функции.
Ауд.: ОЛ-3 №№ 866, 868, 875, 884, 885,889.
Дома: ОЛ-3 №№ 873, 876, 877, 882, 883, 886, 888.
Занятие 24. Контроль по модулю № 2.
