| Представление | Описание |
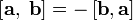
| свойство антикоммутативности |

| свойство ассоциативности относительно умножения на скаляр |

| свойство дистрибутивности по сложению |
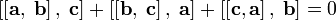
| тождество Якоби, выполняется в 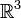 и нарушается в и нарушается в 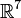
|
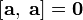
| |
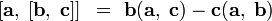
| формула «БАЦ минус ЦАБ», тождество Лагранжа |
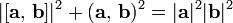
| Это частный случай мультипликативности 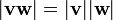 нормы кватернионов нормы кватернионов
|
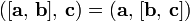
| значение этого выражения называют смешанным произведением векторов  , , 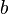 , ,  и обозначают и обозначают 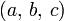 либо либо 
|
№12
Сме́шанное произведе́ние  векторов
векторов 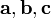 — скалярное произведение вектора
— скалярное произведение вектора 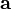 на векторное произведение векторов
на векторное произведение векторов  и
и  :
:
 .
.
Свойства
· Смешанное произведение кососимметрично по отношению ко всем своим аргументам:

т. е. перестановка любых двух сомножителей меняет знак произведения. Отсюда следует, что
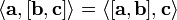
· Смешанное произведение  в правой декартовой системе координат (в ортонормированном базисе) равно определителю матрицы, составленной из векторов
в правой декартовой системе координат (в ортонормированном базисе) равно определителю матрицы, составленной из векторов 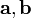 и
и  :
:

· Смешанное произведение  в левой декартовой системе координат (в ортонормированном базисе) равно определителю матрицы, составленной из векторов
в левой декартовой системе координат (в ортонормированном базисе) равно определителю матрицы, составленной из векторов 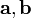 и
и  , взятому со знаком «минус»:
, взятому со знаком «минус»:

В частности,
· Если какие-то два вектора коллинеарны, то с любым третьим вектором они образуют смешанное произведение, равное нулю.
· Если три вектора линейно зависимы (т. е. компланарны, лежат в одной плоскости), то их смешанное произведение равно нулю.
· Геометрический смысл — Смешанное произведение  по абсолютному значению равно объёму параллелепипеда (см. рисунок), образованного векторами
по абсолютному значению равно объёму параллелепипеда (см. рисунок), образованного векторами 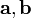 и
и  ; знак зависит от того, является ли эта тройка векторов правой или левой.
; знак зависит от того, является ли эта тройка векторов правой или левой.
· Квадрат смешанного произведения векторов равен определителю Грама, определяемому ими[1]:215.


Три вектора, определяющие параллелепипед.
· Смешанное произведение удобно записывается с помощью символа (тензора) Леви-Чивита:
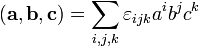
(в последней формуле в ортонормированном базисе все индексы можно писать нижними; в этом случае эта формула совершенно прямо повторяет формулу с определителем, правда, при этом автоматически получается множитель (-1) для левых базисов).
№13
2.1. Определители второго порядка.
Рассмотрим квадратную матрицу 2 × 2
a11 a12
a21 a22
(2.1)
Определение. Определителем второго порядка, соответствующим матрице (2.1),
называется число, равное a11a22 − a12a21 и обозначается как
a11 a12
a21 a22
Таким образом, по определению
a11 a12
a21 a22
= a11a22 − a12a21 (2.2)
Элементы., составляющие матрицу данного определителя, называются элемен-
тами этого определителя.
Покажем, что для того, чтобы определитель второго порядка был равен
нулю, необходимо и достаточно, чтобы элементы его строк (или столбцов) были
пропорциональны.
Действительно, каждая из пропорций a11/a21 = a12/a22 и a11/a12 = a21/a22
эквивалентна равенству a11a22 − a12a21 = 0, а последнее равенство в силу (2.1)
эквивалентно обращению в нуль определителя.
2.2. Определители третьего порядка.
Рассмотрим квадратную матрицу 3 × 3
a11 a12 a13
a21 a22 a23
a31 a32 a33
(2.3)
Определение. Определителем третьего порядка, соответствующим матрице (2.3),
называется число равное
a11a22a33 + a12a23a31 + a13a21a32 −
−a13a22a31 − a11a23a32 − a12a21a33 (2.4)
и обозначаемое символом
a11 a12 a13
a21 a22 a23
a31 a32 a33






