Тригонометрическая форма записи комплексного числа.
Если точка z комплексной плоскости имеет декартовые координаты (х, у), т.е.  и полярные
и полярные  , то они связаны соотношением (1):
, то они связаны соотношением (1):
 .
.
По определению,  и из (1) получаем:
и из (1) получаем:
 . (9)
. (9)
Подставляя в алгебраическую форму записи числа z получаем:  . Или
. Или
 (10)
(10)
Определение. Запись комплексного числа в виде (3) называется еготригонометрической формой.
Замечание. Поскольку одну букву писать экономнее нежели несколько, то чаще всего тригонометрическую форму комплексного числа пишут в виде:
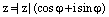 , (11)
, (11)
где  .
.
Теорема. (О равенстве комплексных чисел в тригонометрической форме.)
Два комплексных числа равны тогда и только тогда, когда равны их модули и аргументы.
Доказательство. Так как между всеми комплексными числами и всемиточками комплексной плоскости существует взаимно однозначное соответствие, то равные комплексные числа отождествляются на комплексной плоскости с одной и той же точкой, следовательно, имеют одни и те же полярные координаты, т.е. полярный радиус, который по определению равен модулю комплексного числа, и полярный угол, который по определению равен аргументу комплексного числа. Обратно, если комплексные числа имеют равные модули и аргументы, то они изображаются на комплексной плоскости одной точкой и, следовательно, равны.
Теорема доказана.
Используя соотношения, которые связывают полярные и декартовые координаты точки плоскости, можно найти модуль и аргумент комплексного числа зная его действительную и мнимую части.
Пусть  , т.е.
, т.е.  ,
, 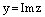 . Тогда
. Тогда
 , (12)
, (12)
 , если точка z лежит в первой или четвертой четверти или
, если точка z лежит в первой или четвертой четверти или  , если точка z лежит во второй или третьей четверти. Также можно пользоваться формулами (6) – (8) п.1, где
, если точка z лежит во второй или третьей четверти. Также можно пользоваться формулами (6) – (8) п.1, где  .
.
Пример. Найти тригонометрическую форму записи комплексного числа z, если:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д) 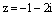 .
.
Решение. а)  ,
,  .
.
 ,
,  .
.
Ответ:  .
.
б)  ,
,  ,
, 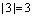 ,
,  .
.
Ответ: 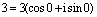 .
.
в)  ,
,  ,
,  ,
,  .
.
Ответ:  .
.
г)  ,
,  ,
,  ,
,  .
.
Ответ:  .
.
д) 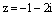 ,
,  ,
,  ,
,
 .
.
Ответ:  , где
, где  .
.
Замечание. В некоторых случаях удобнее не пользоваться формулами, а изображать на чертеже соответствующую точку на комплексной плоскости и находить модуль и аргумент комплексного числа пользуясь чертежом. Например, найдем тригонометрическую форму комплексного числа  .
.
Число 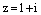 соответствует на комплексной плоскости точке
соответствует на комплексной плоскости точке  . Отметим ее на координатной плоскости:
. Отметим ее на координатной плоскости:

рис.5.
Из рис.5 мы сразу же видим, что  и
и  . Отсюда,
. Отсюда,  .
.
Найдем, далее тригонометрическую форму числа комплексно сопряженного числу  , т.е.
, т.е.  .
.
Из рис.5 мы видим, что  ,
,  и
и
 или
или  .
.
Замечание. Несмотря на то, что  , а
, а 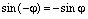 , форма записи комплексного числа z с аргументом
, форма записи комплексного числа z с аргументом  в виде
в виде  не является тригонометрической, т.к.
не является тригонометрической, т.к.  . В этом случае правильной записью тригонометрической формы комплексного числа будет:
. В этом случае правильной записью тригонометрической формы комплексного числа будет:
 или
или  .
.
Умножение комплексных чисел в тригонометрической форме записи. Свойства модуля комплексных чисел.
Теорема. (Об умножении комплексных чисел в тригонометрической форме записи.)
Пусть  , где
, где  и
и  , где
, где  – два произвольных комплексных числа записанных в тригонометрической форме. Тогда
– два произвольных комплексных числа записанных в тригонометрической форме. Тогда
 . (13)
. (13)
Доказательство. 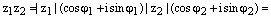

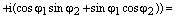
 , ч.т.д.
, ч.т.д.
Теорема доказана.
Отсюда вытекает правило умножения комплексных чисел в тригонометрической форме записи.
Для того, чтобы перемножить два комплексных числа в тригонометрической форме записи нужно перемножить их модули, а аргументы сложить.
Следствие 1. Пусть k натуральное число и  . Пусть далее
. Пусть далее  , где
, где  – произвольные n комплексных чисел записанных в тригонометрической форме записи. Тогда
– произвольные n комплексных чисел записанных в тригонометрической форме записи. Тогда

 .
.
Доказательство проводится индукцией по числу сомножителей и предоставляется читателю.
Следствие 2. Пусть n натуральное число и 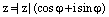 – произвольное комплексное число в тригонометрической форме записи. Тогда
– произвольное комплексное число в тригонометрической форме записи. Тогда
 .
.
Доказательство сразу же следует из Следствия 1.
Теорема. (Свойства модуля комплексного числа.)
Пусть  – произвольные комплексные числа и соответствующие точки на комплексной плоскости. Тогда:
– произвольные комплексные числа и соответствующие точки на комплексной плоскости. Тогда:
1)  и
и  . Т.е. модуль произведения комплексных чисел равен произведению их модулей и модули противоположных чисел равны;
. Т.е. модуль произведения комплексных чисел равен произведению их модулей и модули противоположных чисел равны;
2) расстояние между точками 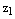 и
и  комплексной плоскости равно модулю разности соответствующих комплексных чисел:
комплексной плоскости равно модулю разности соответствующих комплексных чисел:  ;
;
3)  ;
;
4)  ;
;
Доказательство. 1) По предыдущей теореме имеем:

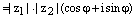 , где
, где  и
и  ,
,
т.е.  .
.
Таким образом, равенства 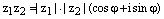 и
и  есть тригонометрическая форма записи числа
есть тригонометрическая форма записи числа  , следовательно, по теореме о равенстве комплексных чисел в тригонометрической форме записи, имеем
, следовательно, по теореме о равенстве комплексных чисел в тригонометрической форме записи, имеем  , ч.т.д.
, ч.т.д.
Далее, т.к.  , то по только что доказанному свойству
, то по только что доказанному свойству 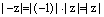 , ч.т.д.
, ч.т.д.
Заметим, что последнее равенство можно получить и из других соображений.
Противоположные числа на комплексной плоскости изображаютсяточками симметричными относительно начала координат. Действительно, пусть  . Тогда
. Тогда  и точки
и точки  ,
,  имеют противоположные декартовые координаты. Значит, в силу симметрии, расстояния от этих точек до начала координат равны, т.е.
имеют противоположные декартовые координаты. Значит, в силу симметрии, расстояния от этих точек до начала координат равны, т.е.  , ч.т.д. Заметим, также, что такой же результат можно получить с помощью формулы (12) вычисления модуля комплексного числа.
, ч.т.д. Заметим, также, что такой же результат можно получить с помощью формулы (12) вычисления модуля комплексного числа.
2). Пусть  ,
,  . Тогда
. Тогда  и по формуле (12) имеем:
и по формуле (12) имеем:
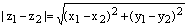 . (14)
. (14)
С другой стороны, рассмотрим числа 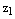 и
и  как точки на комплексной плоскости. Тогда точка
как точки на комплексной плоскости. Тогда точка 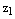 имеет декартовые координаты
имеет декартовые координаты  , а
, а  и искомое расстояние между ними вычисляется по формуле (14), ч.т.д.
и искомое расстояние между ними вычисляется по формуле (14), ч.т.д.
3) Рассмотрим на комплексной плоскости точки 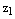 ,
,  и начало координат О. В общем случае эти три точки являются вершинами треугольника
и начало координат О. В общем случае эти три точки являются вершинами треугольника  :
:

рис.6.
Воспользуемся известным свойством треугольника: длина стороны треугольника не превосходит суммы длин двух его других сторон.
Мы только что доказали, что длина стороны  этого треугольника равна
этого треугольника равна  , а длины сторон
, а длины сторон  и
и  равны по определению модулям чисел
равны по определению модулям чисел 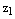 и
и  :
:  ,
,  . Отсюда и получаем, что
. Отсюда и получаем, что  .
.
Заменим в последнем неравенстве число  на противоположное число
на противоположное число 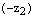 , тогда получаем:
, тогда получаем:
 , ч.т.д.
, ч.т.д.
Заметим, что равенство в этих неравенствах достигается тогда и только тогда, когда треугольник вырождается в отрезок прямой, т.е. когда все три точки О, 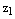 и
и  лежат на одной прямой.
лежат на одной прямой.
4)  , откуда следует
, откуда следует
 . Поменяв местами
. Поменяв местами 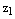 и
и  , получаем
, получаем
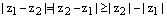 , откуда и следует доказываемое неравенство.
, откуда и следует доказываемое неравенство.
Теорема доказана.
Теория комплексных чисел имеет много приложений в различных областях математики. Не могу удержаться от искушения привести хотя бы один такой пример, относящийся к области теории чисел.
Определение. Говорят, что натуральное число n представимо в виде суммы двух квадратов, если существуют такие целые числа х и у, что выполняется равенство:
 .
.
Теорема. Если два числа представимы в виде суммы двух квадратов, то их произведение также представимо в виде суммы двух квадратов.
Доказательство. Пусть  и
и  , где
, где 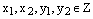 .
.
Нам нужно доказать, что найдутся два целых числа а и b такие, что  .
.
С этой целью рассмотрим два комплексных числа  и
и  .
.
Тогда  и по формуле (12) имеем:
и по формуле (12) имеем:  .
.
С другой стороны,  ,
,  . Так как
. Так как  , то
, то  или
или  , то отсюда получаем равенство:
, то отсюда получаем равенство:  , где
, где  , ч.т.д.
, ч.т.д.
Теорема доказана.






