Определение позиционной игры

В довольно большом классе задач поиска оптимального поведения участников конфликтно-управляемого процесса удобно использовать расширенную форму (дерево целей). описания игры. Расширенная или развернутая форма игры, по существу,. и определяет позиционную игру. Для ее описание используются понятия из теории графов.

Определение. Пара (X,F) называется графом, если X- некоторое конечное множество, а F- отображение X в X.

Граф обозначают символом G. Элементы множества X можно изображать точками на плоскости, а пары точек (x,y=F(x)) соединять непрерывной линией со стрелкой, направленной от x к y. Тогда каждый элемент множества X называется вершиной или узлом графа, а пара элементов (x,y), в которой называется дугой графа. Для дуги q =(x,y) вершины x, y называются граничными вершинами дуги, причем x – начало, а y – конец дуги. Две дуги называются смежными, если они различны и имеют общую граничную точку. Множество дуг в графе обозначают через Q. Задание множества дуг в графе G=(X,F) определяет отображение F и, наоборот, отображение F определяет множество Q. Поэтому граф G можно записывать как в виде G=(X,F), так и в виде G=(X,Q). Путем в графе G называется такая последовательность дуг q= , что конец каждой предыдущей дуги совпадает с началом следующей. Длина пути есть число l(q)=k дуг последовательности. 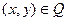Ребром графа G=(X,Q) называется множество из двух элементов для которых или , или Ребра ориентации не имеют (в отличие от дуг). Под цепью понимают последовательность ребер в которой у каждого ребра одна из граничных вершин является также граничной для , а другая – граничной для . Цикл – это конечная цепь, начинающаяся в некоторой вершине и оканчивающаяся в той же вершине. Граф называется связным, если любые две его вершины можно соединить цепью. Дерево или древовидный граф есть конечный связный граф без циклов, имеющий не менее двух вершин. Во всяком дереве существует единственная вершина , такая, что Эту вершину называют начальной вершиной графа G. В общем представлении об игре входят следующие три основных элемента:

1) чередование ходов, которые могут быть как осознанными, так и случайными,

2) возможная недостаточность информации и

3) функция выигрыша.

С учетом вышеприведенных понятий из теории графов под деревом игры будем понимать конечную совокупность узлов, называемых вершинами, соединенных линиями, называемыми ребрами (альтернативами), и при том так, что получается связная фигура, не содержащая простых замкнутых кривых.

Пусть G есть дерево игры с выделенной вершиной А.. Говорят, что вершина С следует за вершиной В, если последовательность ребер, соединяющая А с С, проходит через В. Говорят, что С следует за В непосредственно, если С следует за В и, кроме того, существует ребро, соединяющее В с С. Вершина называется окончательной, если за ней не следует ни одной вершины.

Определение. Под позиционной игрой п лиц понимается следующее:

1) дерево игры G с выделенной вершиной А, называемой начальной позицией игры;

2) функция выигрыша, которая ставит в соответствие каждой окончательной вершине (позиции) дерева G некоторый п- вектор;

3) разбиение множества всех неокончательных вершин (позиций) дерева G на п+1 множеств, называемых множествами очередности;

4) вероятностное распределение для каждой вершины (позиции)на множестве непосредственно следующих за ней вершин (позиций);

5) подразбиение множества вершин (позиций) для каждого игрока i = 1,…,n на подмножества, называемые информационными множествами; при этом вершины (позиции) из одного и того же информационного множества имеют одинаковое число непосредственно следующих за ними позиций (вершин), т.е. альтернатив, и никакая позиция не может следовать за другой позицией из того же самого информационного множества.

Для позиционных игр можно ввести те же определения, что и для игр в нормальной форме (ситуации равновесия и др.). Позиционные игры делятся на многошаговые игры с полной информацией, иерархические игры, многошаговые игры с неполной информацией.

Иерархические игры

Они являются важнейшим подклассом неантагонистических многошаговых игр. С их помощью удобно моделировать конфликтно управляемые системы с иерархической структурой. В математической постановке иерархические игры классифицируются по числу уровней и характеру вертикальных связей. Простейшей из них является двухуровневая система.

Двухуровневая конфликтно управляемая система функционирует следующим образом. Управляющий (координирующий) центр 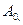находящийся в первом уровне иерархии, выбирает вектор из множества управлений R, где 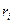- управляющее воздействие центра на подчиненные ему подразделения находящиеся на втором уровне иерархии. В свою очередь, В _i выбирают управления 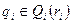, где Q_i (r_i) – множество управлений подразделения B_i, предопределенное управлением r центра А₀. Таким образом, управляющий центр имеет право первого хода и может ограничивать возможности подчиненных ему подразделений, направляя их действия в нужное русло. Цель центра А₀ заключается в максимизации по r функционала 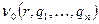, а подразделения B_i, I=1,…,n, обладая собственными целями, стремятся максимизировать по q_i функционалы 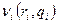.Поставленная задача может быть формализована как задача бескоалиционной игры G (n+1)-го лица (административного центра и производственных подразделений) в нормальной форме. Пусть игрок А₀ выбирает вектор , где

-множество стратегий игрока А₀ в игре G. Вектор r_i будем интерпретировать как набор ресурсов l наименований, выделяемых центром А₀ для I- го производственного подразделения.

Пусть в исходной задаче каждый из игроков B_i,зная выбор А₀, выбирает вектор 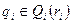, где

.

Вектор q_i интерпретируется как производственная программа I- го производственного подразделения по различным видам продукции; A_i – производственная или технологическая матрица соответствующего подразделения (A_i ³ 0); a_I – вектор наличных ресурсов производственного подразделения (a_I ³ 0).

Под стратегиями игрока B_i в игре будем понимать множество функций q_i (×), ставящих в соответствие каждому элементу r_i вектор . Для игрока А₀ функция выигрыша имеет вид

,

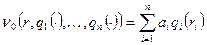где a_i ³ 0. Функцию выигрыша игрока B_i полагаем равной

,

где c_i ³ 0, c_i Î R^m –фиксированный вектор, I = 1,2,…, n.

Построим ситуацию равновесия по Нэшу. Пусть - решение задачи параметрического линейного программирования (параметром является вектор r_i)

,

а -решение задачи

Предположим, что указанные максимумы достигаются. Последняя задача есть задача нелинейного программирования с существенно разрывной целевой функцией (поскольку - разрывные функции параметра r_i).Нетрудно показать, что точка является ситуацией равновесия в игре G. В самом деле,

Далее, при справедливо неравенство

для любой Таким образом никому из игроков не выгодно в одностороннем порядке отклоняться от равновесной ситуации . Можно показать, что эта ситуация также устойчива против отклонения от нее любой коалиции SÌ (B₁,…B_n).

Можно рассматривать кооперативный вариант для иерархических игр. В этом случае строятся характеристические функции и исследуются условия существования непустого С-ядра.

Использованная литература:

Акимов В.П. (2000) Проблема распределения политического влияния и теория кооперативных игр. М: МГИМО(У), 82с..

Беклемишев Д.В. (1974) Курс аналитической геометрии и линейной алгебры, М: Наука.

Бугров Я.С., Никольский С.М. (1985) Высшая математика, М: Наука.

Воробьев Н.Н. (1984) Основы теории игр. Бескоалиционные игры. М: Наука.

Кудрявцев Л.Д. (1973) Математический анализ. Т. 1,2. Москва: «Высшая школа».

Льюис Р., Райфа Х. (1961) Игры и решения. М.: Мир.

Малыхин В.И. (1998) Математическое моделирование экономики, Москва, УРАО.

Малыхин В.И. (1999) Математика в экономике. Москва: ИНФРА-М.

Мулен Э. (1985) Теория игр с примерами из математической экономики. М.: Мир.

Никитина Н.С., Степанов А.В. Математика в экономике. Москва: МГИМО(У).

Петросян Л.А., Зенкевич Н.А., Семина Е.А. (1998) Теория игр. М: “Высшая школа”.

Статистические методы для ЭВМ (по ред. Энслейна К. и др.) (1986) М: Наука.

Фон Нейман Дж., Моргенштерн О. (1970) Теория игр и экономическое поведение. М: Наука.

Owen, G. (1982). Game Theory, Acad.Press.

Ordeshook, P.C. (1986) Game theory and political theory, Cambridge University Press, Cambridge

[1] Dresher, M. (1962) “A sampling inspection problem in arms control agreements: A game theoretic analysis”. Memorandum No/ RM-2972-ARPA. The RAND Corporation, Santa Monica, CA

[2] Shapley, Lloyd S. (1953). A value fили n‑person games, Ann. Math. Studies 28, pages 307‑318.