В момент поступления требования  незавершенная работа, или задолженность системы, совершает скачок на величину
незавершенная работа, или задолженность системы, совершает скачок на величину  , так как это время пройдет до освобождения системы, если не поступит новое требование. С момента
, так как это время пройдет до освобождения системы, если не поступит новое требование. С момента  начинается обслуживание требования
начинается обслуживание требования  , и незавершенная работа убывает со скоростью 1с/c, т. е. функция
, и незавершенная работа убывает со скоростью 1с/c, т. е. функция  убывает с наклоном, равным –1. Через
убывает с наклоном, равным –1. Через  секунд, в момент времени
секунд, в момент времени 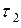 поступает новое требование
поступает новое требование  , что приводит к новому скачку незавершенной работы на величину
, что приводит к новому скачку незавершенной работы на величину  , равную времени обслуживания требования
, равную времени обслуживания требования  . Затем функция снова убывает со скоростью 1с/c, и так до тех пор, пока поступление требования
. Затем функция снова убывает со скоростью 1с/c, и так до тех пор, пока поступление требования  не приведет к новому скачку на величину
не приведет к новому скачку на величину  в точке
в точке  . Функция
. Функция  продолжает убывать, пока работает обслуживающий прибор, т. е. пока в момент
продолжает убывать, пока работает обслуживающий прибор, т. е. пока в момент  не завершается обслуживание всех поступивших требований и система не остается пустой. В этот момент кончается период занятости и начинается новый период простоя. Период простоя кончается в момент времени
не завершается обслуживание всех поступивших требований и система не остается пустой. В этот момент кончается период занятости и начинается новый период простоя. Период простоя кончается в момент времени  , когда поступает требование
, когда поступает требование  . Второй период занятости характеризуется обслуживанием только одного требования, а затем снова наступает период простоя. За третий период занятости обслуживаются два требования, и т.д.
. Второй период занятости характеризуется обслуживанием только одного требования, а затем снова наступает период простоя. За третий период занятости обслуживаются два требования, и т.д.
Для наглядности на рисунке б) дано обычное изображение той же последовательности требований в системе двух осей времени. На одной из этих отмечены моменты времени поступлений, а на другой – время обслуживания требований в том же масштабе, что и на рис. а), в предположении обслуживания в порядке поступления.
Таким образом, функция  представляет собой ломанную линию с вертикальными скачкам и в моменты поступления требования (величина каждого скачка равна соответствующему времени обслуживания), убывающую со скоростью 1с/c до тех пор, пока она положительна. Достигнув значения нуль, функция сохраняет его до поступления следующего требования.
представляет собой ломанную линию с вертикальными скачкам и в моменты поступления требования (величина каждого скачка равна соответствующему времени обслуживания), убывающую со скоростью 1с/c до тех пор, пока она положительна. Достигнув значения нуль, функция сохраняет его до поступления следующего требования.
Как следует из рисунка а), моменты уходов могут быть получены, если продолжить убывающие куски  до пересечения с горизонтальной осью. В эти моменты обслуженные требования уходят, и начинается новое обслуживание. Подчеркнем, что это замечание относится только к дисциплине обслуживания в порядке поступления. Важно, однако, отметить, что сама функция
до пересечения с горизонтальной осью. В эти моменты обслуженные требования уходят, и начинается новое обслуживание. Подчеркнем, что это замечание относится только к дисциплине обслуживания в порядке поступления. Важно, однако, отметить, что сама функция  не зависит от дисциплины обслуживания! Это утверждение будет справедливым, если прибор остается занятым, пока в системе имеются требования, и если не одно требование не покидает прибор до полного завершения его обслуживания. Такая система называется “сохраняющей работу”.
не зависит от дисциплины обслуживания! Это утверждение будет справедливым, если прибор остается занятым, пока в системе имеются требования, и если не одно требование не покидает прибор до полного завершения его обслуживания. Такая система называется “сохраняющей работу”.
Период простоя системы
Вспомним, что

где  и
и  не зависят от n.
не зависят от n.
Нас интересуют распределения
 – распределение периода простоя;
– распределение периода простоя;
 – распределение периода занятости.
– распределение периода занятости.
Вычисление распределения периода простоя для системы M/G/1 тривиально. Заметим, что когда система выходит из периода занятости, начинается новый период простоя, который длится вплоть до поступления следующего требования. Так как процесс поступления требований не имеет последействия, то время до следующего требования распределено по пуассоновскому закону, и поэтому
 .
.
Теперь о периоде занятости; это далеко не так просто.

Рисунок 2. Период занятости: обслуживание в обратном порядке:
а – разложение периода занятости; б – число требований в системе;
В – история требований
Рассмотрим рисунок 2. На рис. 2а) опять рассматривается незавершенная работа  . Предположим, что система свободна вплоть до момента
. Предположим, что система свободна вплоть до момента  , когда требование
, когда требование  начинает период занятости продолжительностью Y. Время обслуживания этого требования равно
начинает период занятости продолжительностью Y. Время обслуживания этого требования равно  . Очевидно, что это требование покинет систему в момент
. Очевидно, что это требование покинет систему в момент  . За время его обслуживания в систему могут поступить другие требования, которые продлят период занятости. Как видно из рисунка, в рассматриваемом примере за время обслуживания требования
. За время его обслуживания в систему могут поступить другие требования, которые продлят период занятости. Как видно из рисунка, в рассматриваемом примере за время обслуживания требования  поступают три других требования (
поступают три других требования ( ,
,  и
и 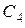 ). Воспользуемся прекрасной схемой, предложенной Такачем. В частности поменяем порядок обслуживания и введем дисциплину обслуживания в обратном порядке (продолжительность периода занятости не зависит от порядка обслуживания).
). Воспользуемся прекрасной схемой, предложенной Такачем. В частности поменяем порядок обслуживания и введем дисциплину обслуживания в обратном порядке (продолжительность периода занятости не зависит от порядка обслуживания).
При уходе требования  на обслуживание поступает последнее требование, в нашем случае
на обслуживание поступает последнее требование, в нашем случае 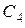 . Кроме того, так как все последующие требования этого периода занятости должны быть обслужены раньше любого требования (кроме
. Кроме того, так как все последующие требования этого периода занятости должны быть обслужены раньше любого требования (кроме 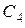 ), поступившего за время облуживания
), поступившего за время облуживания  (в нашем примере
(в нашем примере  и
и  ), последние можно рассматривать (временно) как находящиеся вне системы. Тогда, поступая на обслуживание, требование
), последние можно рассматривать (временно) как находящиеся вне системы. Тогда, поступая на обслуживание, требование 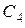 как бы начинает новый период занятости, который назовем подпериодом занятости. Подпериод занятости, порожденный требованием
как бы начинает новый период занятости, который назовем подпериодом занятости. Подпериод занятости, порожденный требованием 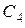 , будет иметь продолжительность
, будет иметь продолжительность  , точно такую же, как время обслуживания этого требования и всех новых требований, которые, поступая в систему, застают ее занятой (при этом требования
, точно такую же, как время обслуживания этого требования и всех новых требований, которые, поступая в систему, застают ее занятой (при этом требования  и
и  ) не учитываются. Таким образом, на рисунке 2 показан подпериод занятости, порожденный требованием
) не учитываются. Таким образом, на рисунке 2 показан подпериод занятости, порожденный требованием 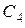 , в течение которого обслуживаются в указанном порядке требования
, в течение которого обслуживаются в указанном порядке требования 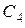 ,
,  и
и 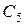 . В момент
. В момент  этот подпериод занятости кончается, и продолжается тот же обратный порядок обслуживания, применяемый теперь к возвращенному в систему требованию
этот подпериод занятости кончается, и продолжается тот же обратный порядок обслуживания, применяемый теперь к возвращенному в систему требованию  . Очевидно, его можно рассматривать как порождающее свой собственный подпериод занятости продолжительностью
. Очевидно, его можно рассматривать как порождающее свой собственный подпериод занятости продолжительностью  , за который в обратном порядке (а именно
, за который в обратном порядке (а именно  ,
,  ,
, 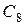 и
и  ) обслуживаются все его “потомки”. Наконец, когда система снова оказывается пустой, возвращается требование
) обслуживаются все его “потомки”. Наконец, когда система снова оказывается пустой, возвращается требование  и начинается его подпериод занятости (длиной
и начинается его подпериод занятости (длиной  ), которым завершается основной период занятости и в течение которого обслуживаются требования
), которым завершается основной период занятости и в течение которого обслуживаются требования  ,
,  и, наконец
и, наконец  .
.
Рисунок 2а) показывает, что очертание любого подпериода занятости повторяет в точности очертание главного периода занятости над тем же промежутком времени и только сдвинуто на постоянную величину. Этот сдвиг равен суммарному времени обслуживания всех тех требований, которые поступили за время обслуживания требования  и которые образуют собственные подпериоды занятости. Общее число требований в системе в любой момент времени при рассматриваемой дисциплине обслуживания показано на рисунке 2б).
и которые образуют собственные подпериоды занятости. Общее число требований в системе в любой момент времени при рассматриваемой дисциплине обслуживания показано на рисунке 2б).
Таким образом, поскольку речь идет о СМО, постольку – это строго система облуживания в обратном порядке, от начала и до конца. Однако анализ упрощается, если сосредоточить внимание на подпериодах занятости и заметить, что каждый из них статистически подобен главному периоду занятости, порожденномутребованием  . Это очевидно, поскольку все подпериоды занятости также, как и главный период занятости, начинаются с появления одного требования; при этом все требования независимы и имеют одно и то же распределение времени обслуживания. Каждый подпериод занятости продолжается до тех пор, пока система не сбрасывает нагрузку в том смысле, что незавершенная работа
. Это очевидно, поскольку все подпериоды занятости также, как и главный период занятости, начинаются с появления одного требования; при этом все требования независимы и имеют одно и то же распределение времени обслуживания. Каждый подпериод занятости продолжается до тех пор, пока система не сбрасывает нагрузку в том смысле, что незавершенная работа  падает до нуля. Таким образом, случайные величины
падает до нуля. Таким образом, случайные величины 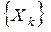 независимы, одинаково распределены и имеют ту же функцию распределения, что и главный период занятости Y.
независимы, одинаково распределены и имеют ту же функцию распределения, что и главный период занятости Y.
Теперь наша точка зрения ясна: продолжительность Y периода занятости является суммой 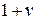 случайных величин, первая из которых – время обслуживания требования
случайных величин, первая из которых – время обслуживания требования  , а остальные описывают подпериоды занятости, каждый из которых распределен так же, как и сам период занятости. Случайная величина
, а остальные описывают подпериоды занятости, каждый из которых распределен так же, как и сам период занятости. Случайная величина 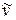 равна числу поступающих требований за время обслуживания требования
равна числу поступающих требований за время обслуживания требования  . Отсюда получается важное соотношение
. Отсюда получается важное соотношение
 .
.
Обозначим функцию распределения периода занятости
 .
.
Из предыдущего известно, что  имеет функцию распределения
имеет функцию распределения  , а
, а  – функцию распределения
– функцию распределения  . Введем преобразование Лапласа для плотности распределения, связанного с Y:
. Введем преобразование Лапласа для плотности распределения, связанного с Y:
 .
.
Воспользуемся теперь мощной техникой условных распределений, часто применяемой в теории вероятностей. Эта техника позволяет записать вероятность, связанную со сложным событием, через условные вероятности этого события при соответствующих условиях, для которых условная вероятность может быть вычислена. Если эти условия несовместимы и исчерпывающи, то безусловную вероятность находят по формуле полной вероятности как сумму произведений условных вероятностей на вероятности условий. В нашем случае будем рассматривать Y в зависимости от двух условий: длительности обслуживания требования  и числа поступающих за время его обслуживания новых требований. Затем выполним следующие условные преобразования:
и числа поступающих за время его обслуживания новых требований. Затем выполним следующие условные преобразования:
 .
.
Поскольку длительности подпериодов занятости взаимно независимы, последнее равенство можно переписать в виде
 .
.
Так как x – заданная постоянная величина, то  , и, кроме того, так как подпериоды занятости распределены одинаково с соответствующим преобразованием
, и, кроме того, так как подпериоды занятости распределены одинаково с соответствующим преобразованием  , то
, то
 .
.
Поскольку 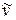 представляет собой число поступающих требований за время x, то эта величина распределена по закону Пуассона со средним значением
представляет собой число поступающих требований за время x, то эта величина распределена по закону Пуассона со средним значением  . Поэтому можно убрать условие, налагаемое на
. Поэтому можно убрать условие, налагаемое на 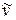 , следующим образом:
, следующим образом:

Точно так же можно убрать условие, налагаемое на  , интегрируя с интегрирующей функцией
, интегрируя с интегрирующей функцией  , чтобы в конце концов, получить
, чтобы в конце концов, получить  в виде
в виде

В последнем выражении легко узнать преобразование плотности распределения времени обслуживания, вычисленного для значения, стоящего в скобках в показателе степени, т. е.
 . (*)
. (*)
Этот главный результат дает преобразование распределения периода занятости для системы M/G/1 (при любом порядке обслуживания), выраженное функциональным уравнением (которое обычно нельзя обратить). Указанное равенство было получено в результате рассмотрения подпериодов занятости, причем эти подпериоды имеют то же распределение, что и сам период занятости.
Ввиду трудностей, связанных с обращением преобразования, найдем, что удастся, прямо из функционального уравнения; в частности, вычислим моменты периода занятости.
Определим  как k -й момент распределения периода занятости. Мы намерены получить первые два момента, выраженных через моменты времени обслуживания
как k -й момент распределения периода занятости. Мы намерены получить первые два момента, выраженных через моменты времени обслуживания  . Имеем по определению
. Имеем по определению
 ;
;
 .
.
Из уравнения (*) непосредственно получаем

Заметим, что при 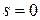 также
также  , поэтому
, поэтому
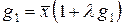 .
.
Решая относительно  и учитывая, что
и учитывая, что  , получаем
, получаем
 .
.
Находим, что средняя длина периода занятости для системы M/G/1 равна среднему времени, проводимому требованием в системе M/M/1, и зависит только от  и
и  .
.
Вычислим теперь второй момент периода занятости. Тогда

и, таким образом,
 .
.
Решая относительно  и применяя полученный результат для
и применяя полученный результат для  , получаем
, получаем
 ,
,
и, окончательно,
 .
.
Последний результат дает второй момент периода занятости. Теперь легко вычислить дисперсию периода занятости, обозначаемую через  , в виде
, в виде
 ,
,
или
 ,
,
где  – дисперсия времени обслуживания.
– дисперсия времени обслуживания.
ВЛОЖЕННАЯ ЦЕПЬ МАРКОВА
Рассмотрим метод вложенной цепи Маркова и применим его к изучению системы M/G/1. Можно добиться упрощения, рассматривая не все моменты времени, а лишь специальным образом подобранную последовательность точек на оси времени. Очевидно, эта последовательность должна быть выбрана так, чтобы, задавая число требований в системе в один из таких моментов и обеспечив дальнейшее поступление требований в систему, можно было бы вычислить число требований в системе в следующий принадлежащий последовательности момент. Поэтому необходимо как-нибудь зафиксировать время, уже проведенное требованием в приборе обслуживания.
Как определить последовательность моментов, обладающую этим свойством? Таких последовательностей можно построить сколько угодно. Особенно удобна последовательность моментов ухода обслуженных требований. Очевидно, что, определив число требований в момент, когда обслуженное требование покидает систему, и, прибавив число поступивших позже требований, можно найти число требований в системе для любого момента времени в будущем. Здесь считается, что в момент ухода обслуженного требования время, потраченное на обслуживание следующего требования, равно нулю, так как обслуживание в этот момент только начинается (если система не остается пустой). Более того, предполагается, что никакое другое требование в очереди не получает обслуживания.
Описанный процесс является полумарковским, при котором изменения состояния происходят в момент ухода требований.
Полумарковские процессы. Начнем с обсуждения полумарковских процессов с дискретным временем. Дискретная цепь Маркова характеризуется тем, что в каждом единичном промежутке времени процесс переходит из текущего состояния в некоторое другое (а может быть и в то же самое) состояние. Вероятности перехода совершенно произвольны; однако вытекающее из марковского свойства требование, чтобы переход происходил в каждый единичный промежуток времени, приводит к тому, что время пребывания процесса в данном состоянии подчиняется геометрическому распределению.
Это накладывает существенные ограничения на рассматриваемые процессы. Если же снять это ограничение, т. е. допустить произвольные распределения для времени пребывания процесса в данном состоянии, то это непосредственно приведет к понятию полумарковского процесса с дискретным временем. При этом определяющим будет условие, что разрешаются произвольные распределения вероятностей времени между переходами из одного состояния в другое. Отметим, однако, что с точки зрения моментов изменения состояния процесс ведет себя как обычная цепь Маркова, и фактически можно сказать, что в эти моменты имеет место вложенная цепь Маркова.
Из изложенного непосредственно вытекает определение полумарковского процесса с непрерывным временем. Здесь допускаются переходы из одного состояния в другое в любой произвольный момент времени. Однако в противоположность марковскому процессу, для которого распределение времени пребывания в состоянии является показательным, в данном случае допускается произвольное распределение. Это приводит к процессам значительно более общего вида, которые успешно применяют при исследовании систем массового обслуживания. Относительно моментов времени изменения состояний здесь также появляются вложенные цепи Маркова. Ясно, что класс марковских процессов входит в класс полумарковских процессов.
Определим вложенную цепь Маркова как число требований, имеющихся в системе в момент ухода очередного обслуженного требования. Переходы имеют место только во вложенных точках и образуют дискретное пространство состояний. Распределение времени между переходами равно распределению времени обслуживания  (функция распределения) всякий раз, когда после обслуживания остается, по крайней мере, одно требование, и равно свертке распределения промежутков времени между поступлениями требований (показательного распределения) с
(функция распределения) всякий раз, когда после обслуживания остается, по крайней мере, одно требование, и равно свертке распределения промежутков времени между поступлениями требований (показательного распределения) с  (плотность распределения) в случае, когда уходящее требование оставляет систему пустой (этому соответствует преобразование Лапласа-Стилтьеса
(плотность распределения) в случае, когда уходящее требование оставляет систему пустой (этому соответствует преобразование Лапласа-Стилтьеса 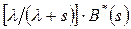 ). Во всяком случае, характеристики цепи в этих вложенных точках полностью описываются марковском процессом, и здесь применимы результаты, рассмотренные ранее (для простейших случайных процессов).
). Во всяком случае, характеристики цепи в этих вложенных точках полностью описываются марковском процессом, и здесь применимы результаты, рассмотренные ранее (для простейших случайных процессов).
Используемый здесь подход состоит в том, чтобы рассматривать исключительно моменты ухода требований и описывать состояние числом требований, остающихся в эти моменты в системе. Решение для вложенных марковских точек обеспечивает решение для всех моментов времени.
Характеризуя состояние системы числом требований в ней, можно наблюдать изменение состояния системы во времени. Если следить за системой непрерывно, можно заметить, что переходы в системе происходят только в соседние состояния. В частности, если состояние системы, содержащей k требований, обозначено через  , то возможны только переходы
, то возможны только переходы  и
и  (причем последний переход возможен лишь при
(причем последний переход возможен лишь при 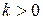 ). Это показано на рис. 1.
). Это показано на рис. 1.

Рис. 1. Переходы для систем с единичным изменением состояний
Заметим теперь, что число переходов типа  отличается не более чем на единицу от числа переходов типа
отличается не более чем на единицу от числа переходов типа  . Первый из этих переходов соответствует поступлению требования и возникает в момент поступления. Второй переход соответствует уходу требования и возникает в момент ухода. После того, как система проработает сколь угодно долго, число переходов вверх должно быть по существу таким же, как число переходов вниз. Так как это движение вверх и вниз относительно
. Первый из этих переходов соответствует поступлению требования и возникает в момент поступления. Второй переход соответствует уходу требования и возникает в момент ухода. После того, как система проработает сколь угодно долго, число переходов вверх должно быть по существу таким же, как число переходов вниз. Так как это движение вверх и вниз относительно  происходит по существу с одной и той же частотой, то отсюда можно заключить, что состояния системы, определяемые уходами требований, имеют то же предельное распределение вероятностей
происходит по существу с одной и той же частотой, то отсюда можно заключить, что состояния системы, определяемые уходами требований, имеют то же предельное распределение вероятностей 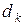 , что и состояния системы, определяемые поступлением требований
, что и состояния системы, определяемые поступлением требований  . Таким образом, обозначив через
. Таким образом, обозначив через  число требований в системе в момент t, можно сделать следующие два вывода.
число требований в системе в момент t, можно сделать следующие два вывода.
1. Для пуассоновского потока требований всегда справедливо равенство
 , т. е.
, т. е.
 .
.
2. Если в некоторой (возможно, немарковской системе) число требований  может быть изменено только на (плюс или минус) единицу, то из существования одного из приведенных ниже распределений следует существование другого и их равенство:
может быть изменено только на (плюс или минус) единицу, то из существования одного из приведенных ниже распределений следует существование другого и их равенство:
 ;
;
 :
:
 .
.
Таким образом, для системы M/G/1 справедливо
 .
.
Далее будет найдено среднее число требований в системе – результат, называемый формулой Полячека-Хинчина для среднего значения. Начнем с введения некоторых обозначений и установим вероятности переходов, связанные с рассматриваемой вложенной цепью Маркова.
ВЕРОЯТНОСТИ ПЕРЕХОДА
Использование моментов времени ухода в качестве вложенных точек на временной оси уже обсуждалось. В эти моменты определяется вложенная марковская цепь как число требований остающихся после ухода. Таким образом, получается полное описание состояний, так как наверняка известно, что вновь поступающее в такой момент требование имеет нулевое время обслуживания, а также, что время, прошедшее после поступления последнего требования, не влияет на будущее развитие процесса, так как распределение промежутков времени между поступлениями – без последействия.
Пусть  означает n -е требование, поступившее в систему;
означает n -е требование, поступившее в систему; 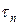 - время поступления
- время поступления  ;
;  - промежуток времени между
- промежуток времени между  и
и  ;
;  - время обслуживания требования
- время обслуживания требования  .
.
Дополнительно введем две важные случайные величины:
 - число требований, остающихся в системе в момент ухода требования
- число требований, остающихся в системе в момент ухода требования  ;
;
 - число требований, поступающих в систему за время обслуживания требования
- число требований, поступающих в систему за время обслуживания требования  .
.
Нас интересует распределение вероятностей  , т.е.
, т.е.  , которое фактически зависит от времени. Предельное (при
, которое фактически зависит от времени. Предельное (при 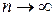 ) распределение
) распределение  совпадает с
совпадает с  , которое равно
, которое равно  - основному распределению вероятностей. При нахождении распределения вероятностей
- основному распределению вероятностей. При нахождении распределения вероятностей  существенную роль будет играть число требований
существенную роль будет играть число требований  , поступивших за время обслуживания одного требования.
, поступивших за время обслуживания одного требования.
Марковская цепь описывается вероятностями перехода; поэтому определим вероятности перехода за один шаг:
 .
.
Поскольку эти переходы наблюдаются только в моменты уходов, ясно, что неравенство 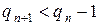 невозможно. С другой стороны, неравенство
невозможно. С другой стороны, неравенство  возможно для всех значений числа поступлений
возможно для всех значений числа поступлений  . Легко видеть, что матрица переходов
. Легко видеть, что матрица переходов  имеет следующий вид:
имеет следующий вид:
 |


где
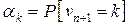 .
.
Например, j -й элемент первой строки матрицы представляет собой вероятность того, что предыдущее требование, уходя, оставило систему пустой, а за время обслуживания требования  поступает ровно j новых требований (и все они остаются в системе после ухода требования
поступает ровно j новых требований (и все они остаются в системе после ухода требования  , но одно из них перемещается в прибор). Точно так же в других строках элемент
, но одно из них перемещается в прибор). Точно так же в других строках элемент  при
при 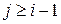 представляет собой вероятность поступления точно
представляет собой вероятность поступления точно  требований за время обслуживания требования
требований за время обслуживания требования  в предположении, что требование
в предположении, что требование  , уходя, оставляет в системе точно i требований (из этих требований одно сразу поступает на обслуживание, что и дает член +1 в последнем расчете). Диаграмма вероятностей перехода для рассматриваемой марковской цепи показана на рис. 2., где изображены только переходы из состояния
, уходя, оставляет в системе точно i требований (из этих требований одно сразу поступает на обслуживание, что и дает член +1 в последнем расчете). Диаграмма вероятностей перехода для рассматриваемой марковской цепи показана на рис. 2., где изображены только переходы из состояния  .
.
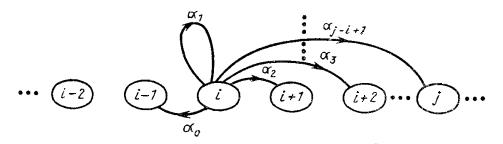
Рис. 2. Диаграмма вероятностей перехода для вложенной марковской цепи
Типа M/G/1
Теперь вычислим  . Заметим, прежде всего, что входящий процесс (пуассоновский поток с интенсивностью
. Заметим, прежде всего, что входящий процесс (пуассоновский поток с интенсивностью  требований в секунду) не зависит от состояния СМО. Точно так же время
требований в секунду) не зависит от состояния СМО. Точно так же время  обслуживания требования
обслуживания требования  не зависит от n и имеет функцию распределения
не зависит от n и имеет функцию распределения  . Следовательно, число
. Следовательно, число 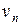 поступлений за время обслуживания
поступлений за время обслуживания  зависит только от продолжительности
зависит только от продолжительности  и не зависит от n. Поэтому можно отбросить индексы у величин
и не зависит от n. Поэтому можно отбросить индексы у величин 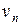 и
и  и заменить их величинами
и заменить их величинами 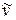 и
и  , так что можно будет записать:
, так что можно будет записать:  и
и  . Перейдем к вычислению
. Перейдем к вычислению  .
.
Применяя условные вероятности, далее получим
 ,
,
где опять  – плотность распределения времени обслуживания. Так как входящий поток является пуассоновским, вероятность, стоящую под знаком интеграла, можно заменить выражением
– плотность распределения времени обслуживания. Так как входящий поток является пуассоновским, вероятность, стоящую под знаком интеграла, можно заменить выражением
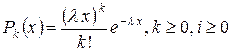 ,
,
что дает
 . (*)
. (*)
Эта формула полностью определяет матрицу вероятностей перехода P.
Заметим, что поскольку  для
для  , все состояния достижимы друг для друга. Введем обычное определение
, все состояния достижимы друг для друга. Введем обычное определение  и подчеркнем, что данная марковская цепь эргодична, если
и подчеркнем, что данная марковская цепь эргодична, если  (чтобы не усложнять рассмотрения, будем в дальнейшем считать это условие выполненным).
(чтобы не усложнять рассмотрения, будем в дальнейшем считать это условие выполненным).
Значительная часть стационарных случайных процессов, с которыми приходится иметь дело на практике, обладает так называемым эргодическим свойством. Это свойство, установленное у стационарных случайных процессов А. Я. Хинчиным, заключается в следующем. Любая вероятностная характеристика процесса, полученная на ансамбле реализаций в какой-либо момент времени t (в одном сечении), равна (с вероятностью, сколь угодно близкой к единице) аналогичной характеристике, полученной на одной единственной реализации процесса путем усреднения по времени за достаточно большой промежуток T.
В следующем параграфе определяется среднее значение  .
.
СРЕДНЯЯ ДЛИНА ОЧЕРЕДИ
В этом разделе выводится формула Полячека-Хинчина для среднего значения длины очереди в пределе. В частности, определяется
 .
.
Этот предел, очевидно, существует в случае, когда рассматриваемая вложенная цепь эргодична.
Сначала выведем уравнения, связывающие случайные величины 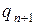 и
и  . Рассмотрим два случая, первый случай показан на рисунке (в обозначениях временной диаграммы) и имеет место тогда, когда уходящее требование
. Рассмотрим два случая, первый случай показан на рисунке (в обозначениях временной диаграммы) и имеет место тогда, когда уходящее требование  не оставляет систему пустой (т. е.
не оставляет систему пустой (т. е.  ).
).

Случай 
Заметим, что предполагается дисциплина обслуживания в порядке поступления, хотя это предположение касается только времени ожидания, а не длины очереди или периода занятости. Из рисунка видно, что  , так как когда требование
, так как когда требование  уходит, требование
уходит, требование 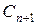 уже находится в системе. На рисунке не показан момент поступления требования
уже находится в системе. На рисунке не показан момент поступления требования  так как это неважно для рассматриваемой задачи. Теперь необходимо найти выражение для
так как это неважно для рассматриваемой задачи. Теперь необходимо найти выражение для  – числа требований, остающихся после ухода требования
– числа требований, остающихся после ухода требования 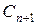 . Оно, очевидно, равно
. Оно, очевидно, равно  (так как требование
(так как требование 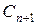 уходит) плюс число требований, поступающих за время обслуживания
уходит) плюс число требований, поступающих за время обслуживания 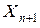 . Это последнее слагаемое, по определению, равно
. Это последнее слагаемое, по определению, равно 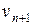 и на диаграмме показано светлой стрелкой. Таким образом, имеем
и на диаграмме показано светлой стрелкой. Таким образом, имеем
 .
.
Рассмотрим теперь второй случай, когда  , т.е. уходящее требование оставляет систему пустой.
, т.е. уходящее требование оставляет систему пустой.

Случай 
Здесь  , очевидно, равно нулю, так как
, очевидно, равно нулю, так как 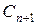 еще не поступило к моменту ухода
еще не поступило к моменту ухода  . Следовательно, число требований
. Следовательно, число требований  , остающихся в момент ухода требований
, остающихся в момент ухода требований 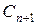 , равно числу поступлений за время его обслуживания. Таким образом,
, равно числу поступлений за время его обслуживания. Таким образом,
 .
.
Объединяя два предыдущих выражения, получаем
 (1)
(1)
Здесь удобно ввести 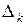 – сдвинутую ступенчатую дискретную функцию
– сдвинутую ступенчатую дискретную функцию
 (2)
(2)
которая связана с дискретной ступенчатой функцией  , определенной равенством
, определенной равенством  .
.
Посредством единичной функции 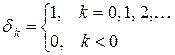 можно учесть тот факт, что когда узел пуст, то интенсивность обслуживания должна равняться нулю.
можно учесть тот факт, что когда узел пуст, то интенсивность обслуживания должна равняться нулю.
Применяя это определение к равенству (1), можно теперь записать единое определяющее соотношение для  в виде
в виде
 . (3)
. (3)
Графики функций 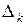 и
и 
 |
Это уравнение является ключевым уравнением для исследования систем M/G/1. Остается получить из него среднее значение величины  . Как обычно, мы не будем касаться характеристик системы, зависящих от времени (эта зависимость заключена в индексе n), а будем искать сразу распределение предельной величины
. Как обычно, мы не будем касаться характеристик системы, зависящих от времени (эта зависимость заключена в индексе n), а будем искать сразу распределение предельной величины  , обозначая ее
, обозначая ее  . Предположим, что в пределе, при
. Предположим, что в пределе, при 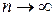 , существует j -й момент
, существует j -й момент  :
:
 (4)
(4)
(мы здесь фактически требуем эргодичности).
Будем считать, что в уравнении (3) операции усреднения и перехода к пределу перестановочны. Беря среднее значение от обеих частей равенства (3), получаем
 .
.
Переходя к пределе при 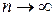 , имеем
, имеем
 ,
,
что после упрощения дает
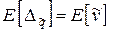 . (5)
. (5)
Какие сведения получаем мы из этого равенства? (Заметим, что поскольку 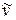 – число требований, поступающих за время одного обслуживания, которое не зависит от n, индекс у величины
– число требований, поступающих за время одного обслуживания, которое не зависит от n, индекс у величины 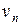 может быть опущен даже до перехода к пределу). По определению
может быть опущен даже до перехода к пределу). По определению  – среднее число требований, поступающих за время одного обслуживания.
– среднее число требований, поступающих за время одного обслуживания.
Дадим интерпретацию левой части последнего равенства. По определению можно непосредственно вычислить

Но, пользуясь равенством (2), можно переписать это в виде
 ,
,
или
 .
.
Так как мы имеем дело с однолинейной системой, это равенство также может быть записано в виде
 . (6)
. (6)
Пользуясь определением коэффициента нагрузки системы, далее находим
 . (7)
. (7)
Таким образом, на основании равенств (5, 6, 7) заключаем, что
 . (8)
. (8)
Мы получили хорошо обоснованное заключение о том, что ожидаемое число поступающих требований за время одного обслуживания равно  . Для устойчивости системы требуется, чтобы
. Для устойчивости системы требуется, чтобы  ; таким образом, равенство (8) означает, что в среднем требования должны поступать медленнее, чем они могут быть обслужены.
; таким образом, равенство (8) означает, что в среднем требования должны поступать медленнее, чем они могут быть обслужены.
Вернемся теперь к среднему значению величины  . Взяв математические ожидания от обеих частей уравнения (3) и переходя к пределу, мы не смогли получить эту величину, хотя и получили интересные результаты. Чтобы найти искомое среднее значение, введем (3) сначала в квадрат, а уже затем определим математическое ожидание от обеих частей полученного равенства:
. Взяв математические ожидания от обеих частей уравнения (3) и переходя к пределу, мы не смогли получить эту величину, хотя и получили интересные результаты. Чтобы найти искомое среднее значение, введем (3) сначала в квадрат, а уже затем определим математическое ожидание от обеих частей полученного равенства:
 . (9)
. (9)
Из определения (2) следует, что  и
и  . Учитывая это и вычисляя математические ожидания в (9), получаем
. Учитывая это и вычисляя математические ожидания в (9), получаем

В этом равенстве в двух последних слагаемых справа имеется произведение двух случайных величин, стоящее под знаком математического ожидания. Однако заметим, что  (число поступлений за время обслуживания
(число поступлений за время обслуживания  -го требования) не зависит от
-го требования) не зависит от  (числа требований, остающихся после ухода требования
(числа требований, остающихся после ухода требования  ). Следовательно, в обоих слагаемых математическое ожидание произведения равно произведению математических ожиданий. Переходя к пределу с учетом (4), получаем
). Следовательно, в обоих слагаемых математическое ожидание произведения равно произведению математических ожиданий. Переходя к пределу с учетом (4), получаем

Используем теперь (5) и (8), чтобы получить следующий вспомогательный результат:
 ; (10)
; (10)
здесь неизвестно только  .
.
Вычисляя эту величину, попутно укажем метод нахождения моментов любого порядка. Для этого целесообразно ввести производящую функцию случайной величины 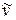 :
:
 . (11)
. (11)
Образую функцию  из (*) и (11), получим (*)
из (*) и (11), получим (*) 
 .
.
Здесь операции суммирования и интегрирования перестановочны. Меняя порядок операций, получаем
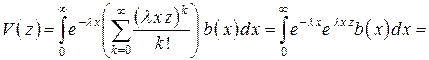
 . (12)
. (12)
Введем теперь преобразование Лапласа плотности времени обслуживания
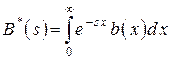 .
.
Заметим, что равенство (12) дает выражение такого же вида с заменой комплексной переменной  на
на  . Получается важный результат
. Получается важный результат
 (13)
(13)
Найденное равенство чрезвычайно важно. Оно описывает связь между производящей функцией распределения вероятностей случайной величины 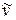 и преобразованием Лапласа плотности распределения случайной величины
и преобразованием Лапласа плотности распределения случайной величины  , когда это преобразование находится в критической точке
, когда это преобразование находится в критической точке  . Вспомним, что
. Вспомним, что 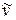 – это число требований, поступающих за промежуток времени
– это число требований, поступающих за промежуток времени  , и что поток поступающих требований является пуассоновским с интенсивностью
, и что поток поступающих требований является пуассоновским с интенсивностью  требований в секунду.
требований в секунду.
Различные производные, вычисленные в точке  , дают возможность вычислить соответствующие моменты рассматриваемой случайной величины. Точно так же для непрерывных случайных величин можно найти моменты, вычисляя в точке
, дают возможность вычислить соответствующие моменты рассматриваемой случайной величины. Точно так же для непрерывных случайных величин можно найти моменты, вычисляя в точке  соответствующие производные преобразования Лапласа плотности рассматриваемой случайной величины. В частности,
соответствующие производные преобразования Лапласа плотности рассматриваемой случайной величины. В частности,
 ; (14)
; (14)
 ; (15)
; (15)
 . (16)
. (16)
Чтобы упростить обозначения, мы не переходим к пределу после дифференцирования, а сразу подставляем предельные значения аргументов. Далее мы обозначаем чертой сверху математическое ожидание случайной величины, стоящей под чертой. Тогда равенства (14) – (16) примут вид
 ; (17)
; (17)
 ; (18)
; (18)
 . (19)
. (19)
Конечно, при этом должно сохраняться свойство вероятностей
 . (20)
. (20)
Применяя теперь равенство (13), постараемся из выражений (17) – (20) получить моменты случайной величины 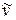 . Дифференцируя (13), получаем
. Дифференцируя (13), получаем
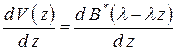 . (21)
. (21)
Производная, стоящая справа, может быть вычислена в виде
 , (22)
, (22)
где 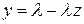 . (23)
. (23)
Полагая в (21)  , получим
, получим
 .
.
Но из (23) следует, что частный случай  соответствует случаю
соответствует случаю  , поэтому
, поэтому
 . (24)
. (24)
Наконец, из (17), (18) и (24) окончательно получается
 . (25)
. (25)
Но  – это точно
– это точно  , и мы снова получили тот же результат, что и в равенстве (8), а именно
, и мы снова получили тот же результат, что и в равенстве (8), а именно  . Можно продифференцировать (21), чтобы получить
. Можно продифференцировать (21), чтобы получить
 . (26)
. (26)
Применяя полученную ранее первую производную функции  , получим теперь вторую производную следующим образом:
, получим теперь вторую производную следующим образом:
 ,
,
или
 . (27)
. (27)
Подставляя в (26)  и используя (27), получаем
и используя (27), получаем
 .
.
Сравнивая последний с полученными ранее результатами (17) и (19), находим
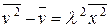 , (28)
, (28)
что дает окончательно решение для  . Таким образом, получена величина, необходимая для подстановки в (10).
. Таким образом, получена величина, необходимая для подстановки в (10).
Возвращаясь к равенству (10), используем (28) и получим
 . (29)
. (29)
Это и есть результат, к которому мы стремились! Он выражает среднюю длину очереди в момент ухода обслуженного требования через известные величины, а именно через коэффициент использования ( ),
),  и
и  (второй момент распределения времени обслуживания). Перепишем этот результат, введя нормированную дисперсию времени обслуживания
(второй момент распределения времени обслуживания). Перепишем этот результат, введя нормированную дисперсию времени обслуживания  :
:
 . (30)
. (30)
Это выражение представляет собой очень известную формулу для среднего числа требований в системе типа M/G/1, которую обычно называют формулой Полячека-Хинчина для среднего значения. Подчеркнем, что среднее значение зависит только от первых двух моментов распределения времени обслуживания ( и
и  ). Кроме того, заметим, что
). Кроме того, заметим, что  возрастает линейно с ростом дисперсии времени обслуживания (или, если угодно, линейно с квадратом его коэффициента вариации).
возрастает линейно с ростом дисперсии времени обслуживания (или, если угодно, линейно с квадратом его коэффициента вариации).
Формула Полячека-Хинчина позволяет найти среднее число требований в системе в моменты ухода обслуженного требования. Однако, как уже известно, она позволяет найти и среднее число требований в моменты их поступления и в любые другие моменты времени. Ранее было введено обозначение  для среднего числа требований в системе. Кроме того, было определено
для среднего числа требований в системе. Кроме того, было определено 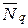 – среднее число требований в очереди (не считая обслуживаемого требования). Найдем связь между
– среднее число требований в очереди (не считая обслуживаемого требования). Найдем связь между  и
и 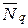 . По определению
. По определению
 , (31)
, (31)
 .
.
Длина очереди на единицу меньше числа требований в системе, если система не пуста, поэтому
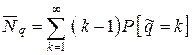 ,
,

(Обратите внимание на нижний предел суммирования.) Отсюда получаем
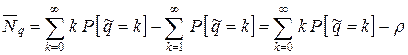 .
.
После вычитания этих двух рядов и получается второе слагаемое.
Но вторая сумма равна  , и мы приходим к равенству
, и мы приходим к равенству
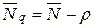 . (32)
. (32)
Эта простая формула и устанавливает искомую связь.
В качестве примера применения формулы Полячека-Хинчина рассмотрим систему типа M/M/1. Так как для показательного распределения коэффициент вариации равен единице, то для такой системы
 ,
,
или
 , M/M/1. (33)
, M/M/1. (33)
Равенство (33) описывает ожидаемое число требований, остающихся при уходе обслуженного требования. Сравним его с выражением для среднего числа требований в системе M/M/1. Эти формулы идентичны, и это лишний раз подтверждает приводившееся ранее утверждение о том, что метод вложенных цепей Маркова в случае СМО типа M/G/1 дает решение, пригодное для любого момента времени.
В качестве второго примера рассмотрим регулярное обслуживание с постоянным временем обслуживания  . Как уже отмечалось, такие системы обозначаются через M/D/1. В этом случае, очевидно
. Как уже отмечалось, такие системы обозначаются через M/D/1. В этом случае, очевидно  , и получается
, и получается
 ; (34)
; (34)
 , M/D/1.
, M/D/1.
Таким образом, система типа M/D/1 в среднем содержит на  требований меньше, чем система M/M/1; это иллюстрирует сделанное ранее утверждение о том, что q убывает с убыванием дисперсии времени обслуживания.
требований меньше, чем система M/M/1; это иллюстрирует сделанное ранее утверждение о том, что q убывает с убыванием дисперсии времени обслуживания.
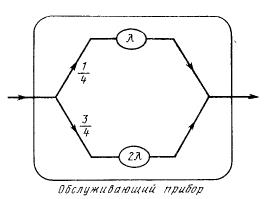
Рисунок. Пример системы M/H2/1
Наконец, в качестве третьего примера рассмотрим систему M/H2/1, в которой
 . (35)
. (35)
Это значит, что прибор обслуживания состоит из двух параллельных этапов, как показано на рисунке.
Заметим также, что как обычно,  – интенсивность поступления требований. М
– интенсивность поступления требований. М






