Свойство отсутствия памяти с предположение о независимости интервалов между поступлениями и длительностью обслуживания означают, что если известно 
, т. е. число требований в системе в момент, то будущие моменты поступления или завершения обслуживания не зависят от моментов поступления требований, которые находятся в данный момент в системе, и от того, сколько времени уже обслуживалось требование, которое в данный момент находится в обслуживающем приборе (если таковое имеется). Это означает, что 
является цепью Маркова с непрерывным временем (марковским процессом).
Мы могли бы рассматривать процесс в терминах теории цепей Маркова с непрерывным временем как в большей части литературы по системам массового обслуживания. Однако для наших целей в этом разделе достаточно использовать более простую теорию цепей Маркова с дискретным временем.
Обратим внимание на моменты
где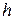 
– малое положительное число. Введем обозначение 
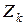– число требований в системе в момент 
. Поскольку – цепь Маркова с непрерывным временем, получаем что 
– цепь Маркова с дискретным временем. Обозначим через 
соответствующие переходные вероятности
.
Получаем
, (1)
, (2)
, (3)
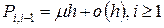, (4)
.
В состоянии 
вероятность того, что в интервале 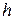не поступит ни одно требование и ни одно требование не уйдет из системы, равна 
. Это следует из того, что число поступлений и число уходов имеют пуассоновское распределение и не зависят друг от друга. Разлагая эту вероятность в ряд по 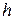, получаем
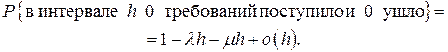(5)
Аналогично имеем, что
,
.
Сумма этих вероятностей равна единице плюс 
. Таким образом, вероятность более чем одного поступления или ухода пренебрежимо мала при малых 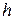. Это означает, что 
– вероятность одинакового числа поступлений и уходов в интервале 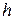с точностью до совпадает с вероятностью (5); это показывает справедливость равенства (2). Соотношения (1), (3), (4) устанавливаются аналогичным образом.
Диаграмма переходов из состояния в состояние цепи Маркова показана на рис. 1, на нем члены опущены.
Рис. 1. Цепь Маркова с дискретным временем для системы M / M /1. Состояние 
соответствует наличию требований в системе. Переходные вероятности показаны с точностью 
до члена
Рассмотрим теперь стационарные вероятности
.
Заметим, что при любых 
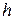в течение времени от до общее число переходов из состояния 
в состояние 
(в одну и другую сторону) должно отличаться не более чем на 1. Аналогично общее число переходов из состояния в состояние (в одну и другую сторону) также должно отличаться не более чем на 1. Таким образом, в стационарном режиме вероятность того, что система находится в состоянии и при следующем переходе попадает в состояние , равна вероятности того, что система находится в состоянии и делает переход в состояние , т. е.
. (6)
Так как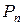 
не зависит от 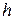, устремляя 
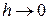, получаем
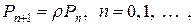где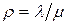 
.
Отсюда следует, что
. (7)
Если 
(скорость обслуживания превышает скорость поступлений, а сумма вероятностей 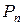равна единице), то
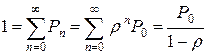. (8)
Это соотношение вместе с формулой (7) окончательно дает
. (9)
Теперь можно вычислить среднее число требований в системе в стационарном режиме
и, наконец, используя равенство 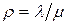, получаем
. (10)
Это равенство показано графически на рис. 2. При увеличении 
значение 
также увеличивается и при 
имеем 
. График справедлив при 
. Если 
, обслуживающий прибор не может справиться с потоком поступлений требований и очередь неограниченно возрастает. В терминах системы пакетной передачи означает, что 
, где 
– скорость поступления (в числе пакетов в секунду), 
– средняя длина пакета в битах, 
– пропускная способность канала в битах в секунду.
Средняя задержка требования (время ожидания в очереди плюс время обслуживания), согласно теореме Литтла, равна
. (11)
Подставляя 
, получаем
. (12)
Среднее время ожидания в очереди 
равно средней задержке пакета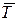 
минус среднее время обслуживания 
, поэтому
.
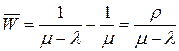Из теоремы Литтла получаем, что среднее число требований в очереди равно
.
Очень полезно рассматривать величину как коэффициент использования системы массового обслуживания, т. е. как стационарную долю времени, в течение которой занят обслуживающий прибор. Мы этот коэффициент можем рассматривать по-другому. Имеем 
, где 
– вероятность того, что в системе нет требований; получается другое доказательство для формулы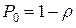 
.
Проиллюстрируем эти результаты на некоторых примерах, относящихся к сетям передачи данных.
Пример. Увеличение скорости поступления и скорости передачи в одинаковое число раз
Рассмотрим систему пакетной передачи, в которой скорость поступления (в пакетах в секунду) увеличивается от до 
, где 
– некоторый числовой коэффициент. Распределение длины пакетов остается неизменным, а пропускная способность возрастает в раз, так что среднее время передачи пакета становится равным 
вместо . Отсюда следует, что коэффициент использования линии и, следовательно, среднее число пакетов в системе остаются неизменными
.
Однако средняя задержка пакета теперь будет равна 
и, следовательно, уменьшается в раз. Иначе говоря, линия передачи, которая передает в K раз быстрее, будет передавать в K раз больше пакетов в секунду со средней задержкой пакета в K раз меньшей. Этот результат общий и даже применим к сетям связи. Как показано на рис. 3, при увеличении скорости поступления и скорости обслуживания в K раз вероятностные характеристики процесса массового обслуживания не изменяются, за исключением временного масштаба – процесс ускоряется в K раз. Таким образом, когда пакет поступает в систему, он обнаруживает перед собой в вероятностном смысле такое же число пакетов, как и в случае низкоскоростной линии передачи. Однако пакеты, стоящие впереди него, будут продвигаться в K раз быстрее.
 | |||
 |
Рис. 3а. Увеличение интенсивности поступления пакетов и скорости обслуживания в одинаковое число раз (исходная диаграмма)
 |
Рис. 3б. Увеличение интенсивности поступления пакетов и скорости обслуживания в одинаковое число раз (диаграмма после увеличения интенсивностей в K раз)
Пример. Статистическое уплотнение по сравнению с временным и частотным уплотнением
Предположим, что 
статистически одинаковых и независимых пуассоновских потоков передаются по линии связи со скоростью 
пакетов в секунду каждый. Длины пакетов во всех потоках независимы и имеют экспоненциальное распределение. Среднее время передачи равно . Если потоки сливаются в один пуассоновский поток с интенсивностью , как это происходит при статистическом уплотнении, средняя задержка пакета становится равной
.
Если вместо этого пропускная способность канала делится на равных частей, по одной для каждого потока пакетов, каждая часть ведет себя как система массового обслуживания M / M /1 со скоростью поступления и средней скоростью обслуживания 
. Следовательно, средняя задержка пакета равна
,
т. е. в раз больше, чем при статистическом уплотнении.
Приведенные соображения показывают, что уплотнение большого числа потоков путем распределения их по отдельным каналам линии передачи является очень неэффективным в смысле задержки.
Эффективность системы становится еще хуже, если пропускная способность каналов распределяется не прямо пропорционально интенсивностям соответствующих потоков; пропорциональное распределение невозможно провести (по крайней мере в модели, которая рассматривается здесь), если интенсивности потоков меняются с течением времени, поэтому сети передачи данных со многими конкурирующими потоками, имеющие малые периоды занятости, строятся на основе некоторой формы статистического уплотнения. Соображения в пользу временного или частотного уплотнения появляются, если все потоки являются регулярными (в противоположность пуассоновскому) в том смысле, что пакет не поступает, если передается другой, и поэтому, если такой поток передается по предназначенной для него линии, пакетов, ожидающих в очереди, нет.
N-КАНАЛЬНАЯ СМО С ОТКАЗАМИ (задача Эрланга)
Имеется каналов (линий связи), на которые поступает поток заявок с интенсивностью . Поток обслуживаний имеет интенсивность 
. Найти финальные вероятности состояний СМО, а также характеристики ее эффективности:
–абсолютную пропускную способность, т.е. среднее число заявок, обслуживаемых в единицу времени;
– относительную пропускную способность, т.е. среднюю долю пришедших заявок, обслуживаемых системой;
– вероятность отказа, т.е. того, что заявка покинет СМО не обслуженной;
– среднее число занятых каналов.
Состояния системы 
будем нумеровать по числу заявок, находящихся в системе (в данном случае оно совпадает с числом занятых каналов):
– в СМО нет ни одной заявки;
– в СМО находится одна заявка (один канал занят, остальные свободны);
…
– в СМО находится k заявок (k – каналов заняты, остальные свободны);
…
– в СМО находится n заявок (все n каналов заняты).
Граф состояний СМО соответствует схеме размножения и гибели.
 |
Из в систему переводит поток с интенсивностью (как только приходит заявка система переходит из состояния в состояние ). Тот же поток заявок переводит систему из любого левого состояния в соседнее правое.
Поставим интенсивности у нижних стрелок. Пусть система находится в состоянии (работает один канал). Он производит обслуживаний в единицу времени. Проставляем у стрелки 
интенсивность . Теперь представим себе, что система находится в состоянии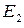 
(работают два канала). Чтобы ей перейти в , нужно, чтобы либо закончил обслуживание первый канал, либо второй; суммарная интенсивность их потоков обслуживаний равна 
; проставляем ее у соответствующей стрелки. Суммарный поток обслуживаний, даваемый тремя каналами, имеет интенсивность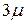 
, k каналами – 
. Проставляем эти интенсивности у нижних стрелок на рисунке.
А теперь, зная все интенсивности, воспользуемся уже готовыми формулами для финальных вероятностей в схеме рождения и гибели
. (1)
Члены разложения 
представляют собой коэффициенты при 
в выражениях для 
:
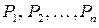. (2)
Заметим, что в формулы (1) и (2) интенсивности и входят не по отдельности, а только в виде отношения 
. Обозначим 
и будем называть величину “приведенной интенсивностью потока заявок”. Ее смысл – среднее число заявок, приходящее за среднее время обслуживания одной заявки. Тогда
, (4)
. (5)
Формулы (4) и (5) для финальных вероятностей состояний называются формулами Эрланга.
Найдем 
– вероятность того, что пришедшая заявка получит отказ (не будет обслужена). Для этого нужно, чтобы все n каналов были заняты, значит,
. (6)
Отсюда находим относительную пропускную способность – вероятность того, что заявка будет обслужена:
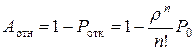. (7)
Абсолютную пропускную способность мы получим, умножая интенсивность потока заявок на :
. (8)
Осталось найти среднее число занятых каналов . Эту величину можно было бы найти “впрямую”, как математическое ожидание дискретной случайной величины с возможными случайными значениями 
и вероятностями этих значений 
:
.
Подставляя сюда выражения (5) для 
и выполняя соответствующие преобразования, мы, в конце концов, получили бы верную формулу для . Но мы выведем ее гораздо проще. В самом деле, нам известна абсолютная пропускная способность . Это – не что иное, как интенсивность потока обслуженных системой заявок. Каждый занятый канал обслуживает в среднем заявок. Значит, среднее число занятых каналов равно
, (9)
или учитывая (8),
.
