Структура системы массового обслуживания

МОДЕЛИ ОЧЕРЕДЕЙ В ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМАХ И СЕТЯХ

 

С целью повышения загрузки (уменьшения простоев) программных и аппаратных ресурсов вычислительных систем (ВС) современная организация вычислительного процесса предусматривает возможность создания к ним очередей. Примером могу служить очередь заданий, ожидающих распределения памяти, очереди заданий к центральному процессору и на ввод-вывод. Ожидающие того или иного вида обслуживания задания (в других случаях это могут быть запросы, сообщения, задачи процессы или программы) будем называть заявками (запросами), а устройство, предназначенное для их обслуживания (например, память, центральный процессор (ЦП), устройство ввода-вывода), – обслуживающим устройством.

В ВС возможны очереди, в которых заявки не являются заданиями в обычном смысле этого слова. Так, например, в мультипроцессорных ВС, как правило, работать данным модулем памяти (производить считывание-запись) в каждый момент времени может только какой-нибудь один ЦП. Таким образом, если в процессе работы одного из ЦП с некоторым модулем памяти к тому возникает запрос от другого ЦП, то он должен подождать освобождения этого модуля памяти. Понятно, что в приведенном примере заявками являются запросы от ЦП, а обслуживающими устройствами – блоки памяти.

При количественном анализе очередей в ВС требуется дать ответ по крайней мере на два вопроса: насколько загружено рассматриваемое обслуживающее устройство и каково время ожидания заявок в очереди? Оба крайних случая, когда обслуживающее устройство занято мало, т.е. подолгу простаивает, и когда загрузка чрезмерно велика, вследствие чего заявки длительное время ожидают обслуживания, требуют принятия корректирующих решений в управлении вычислительным процессом. Поскольку в ВС многие ресурсы взаимосвязаны, излишняя загрузка одного из них и недостаточная загрузка другого могут привести к уменьшению пропускной способности ВС в целом.

Методы решения задач количественного анализа очередей составляют предмет одного из разделов теории вероятностей, известного под названием теория очередей или теория массового обслуживания.

 

СТРУКТУРА СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ

 

Хотя ВС представляет собой взаимосвязанную совокупность вычислительных ресурсов, в ряде случаев основной интерес представляет задача оценки загруженности одного из этих ресурсов, например, центрального процессора, накопителя на магнитных дисках или оператора вычислительной установки (например, сетевого оператора). Эту задачу можно решать в рамках моделей систем массового обслуживания с одним обслуживающим устройством, методы исследований которых составляют наиболее развитый и завершенный раздел теории.

Основные элементы системы массового обслуживания (СМО) показаны на рисунке.

 

 

Структура системы массового обслуживания

 

Обслуживаемой единицей в СМО является заявка. Заявки поступают на обслуживающее устройство. Если поступающие в СМО заявки не могут быть удовлетворены немедленно, то возникает очередь. Очередь присуща не всякой СМО. Существуют такие СМО, которых очередь не допускается, и заявка, заставшая обслуживающее устройство, занятым, теряется. Если в момент поступления заявки обслуживающее устройство занято, то заявка занимает очередь к нему, где ожидает начало обслуживания.

Выбор заявки на обслуживание в какой-то момент времени производится в соответствии с некоторым правилом, которое называется дисциплиной обслуживания. Далее выполняется обслуживание заявки, и после завершения обслуживания заявка покидает систему. Выходящий поток обслуженных заявок может оказаться весьма важным в тех случаях, когда он является входящим для другой СМО. Так, например, программы могут попеременно требовать обслуживания центрального процессора и процессора ввода-вывода.

О таких элементах СМО, как входящий поток заявок, механизм обслуживания и дисциплина обслуживания, можно сделать различные предположения. Остановимся на некоторых из них.

Входящий поток заявок

Пусть теперь – моменты поступления заявок пуассоновского потока. Тогда для любого 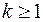функция распределения

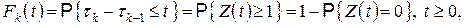
или .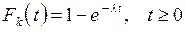

Таким образом, для пуассоновского входящего потока промежутки времени между моментами поступления заявок статистически независимы и имеют одинаковое экспоненциальное распределение.

Для пуассоновского входящего потока имеет место важное свойство отсутствия последействия: время ожидания поступления новой заявки не зависит от того, когда появилась предыдущая заявка. Поскольку интервалы между моментами поступления заявок имеют экспоненциальное распределение, точная формулировка этого свойства является следующей. Пусть случайная величина распределена по экспоненциальному закону, т.е.

Тогда для любого числа

. (1)

В общем случае входящий поток заявок определяется посредством задания для каждого совместного распределения случайных величин , где , а – моменты поступления заявок . В том случае, когда случайные величины 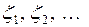независимы в совокупности, для определения входящего потока достаточно задать набор одномерных функций распределения . Такой входящий поток называется потоком с ограниченным последействием. Естественным обобщением пуассоновского потока является поток, для которого 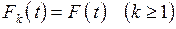. Такой поток называется рекуррентным.

Рассмотрим ординарный поток однородных событий.

 

 

Этот поток называется потоком с ограниченным последействием (или потоком Пальма), если промежутки времени между последовательными событиями представляют собой независимые случайные величины.

Очевидно, простейший поток является частным случаем потока Пальма: в нем расстояния представляют собой независимые случайные величины, распределенные по показательному закону.

Рассмотрим примеры потоков Пальма.

1. Некоторая деталь технического устройства (например, радиолампа) работает непрерывно до своего отказа (выхода из строя), после чего она мгновенно заменяется новой. Срок безотказной работы детали случаен; отдельные экземпляры выходят из строя независимо друг от друга. При этих условиях поток отказов (или поток «восстановлений») представляет собой поток Пальма. Если, к тому же, срок работы детали распределен по показательному закону, то поток Пальма превращается в простейший.

2. Группа самолетов идет в боевом порядке «колонна» с одинаковой для всех самолетов скоростью .

 

Каждый самолет, кроме ведущего, обязан выдерживать строй, т. е. держаться на заданном расстоянии от впереди идущего. Это расстояние, вследствие погрешностей радиодальномера, выдерживается с ошибками. Моменты пересечения самолетами заданного рубежа образуют поток Пальма, так как случайные величины 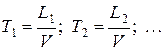независимы. Заметим, что тот же поток не будет потоком Пальма, если каждый из самолетов стремится выдержать заданное расстояние не от соседа, а от ведущего.

Интересным примером потоков с ограниченным последействием являются так называемые потоки Эрланга. Они образуются «просеиванием» простейшего потока.

Рассмотрим простейший поток и выбросим из него каждую вторую точку (на рисунке выброшенные точки отмечены крестами).

 

 

 

Оставшиеся точки образуют поток; этот поток называется потоком Эрланга первого порядка . Очевидно, этот поток есть поток Пальма: поскольку независимы промежутки между событиями в простейшем потоке, то, независимы и величины , получающиеся суммированием таких промежутков по два.

Поток Эрланга второго порядка получится, если сохранить в простейшем потоке каждую третью точку, а две промежуточные выбросить.

 

 

Вообще, потоком Эрланга k -го порядка 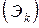называется поток, получаемый из простейшего, если сохранить каждую -ю точку, а остальные выбросить. Очевидно, простейший поток можно рассматривать как поток Эрланга нулевого порядка .

 

Механизм обслуживания

Второй компонентой СМО является количественная характеристика обслуживания, требуемого отдельной заявкой. Назовем эту характеристику длиной заявки. Единица измерения длины заявки меняется в зависимости от природы обслуживающего устройства и заявок. Если обслуживающее устройство – ЦП, а заявки – программы, то длина может измеряться в командах. Если обслуживающее устройство – линия передачи данных, а заявки – передаваемые сообщения или данные, то длина может измеряться в битах или байтах. Если совокупность заявок однородна, то предполагается, что длины различных заявок являются независимыми в совокупности и одинаково распределенными случайными величинами. В более сложных ситуациях заявки можно разделить на несколько различных типов, каждый из которых составит однородную совокупность заявок.

Чтобы задать механизм обслуживания полностью, помимо распределения длин заявок необходимо также задать быстродействие обслуживающего устройства. Обозначим величину быстродействия через C. Единица измерения быстродействия зависит от типа обслуживания. Если обслуживающее устройство – ЦП, то быстродействие измеряется в операциях в секунду. Если обслуживающее устройство – канал или линия передачи данных, то быстродействие, т.е. скорость передачи данных, измеряется в битах в секунду.

Если длина заявки равна S [единиц обслуживания] и она обслуживается устройством с быстродействием C [единиц обслуживания в секунду], то отношение [секунд] называется длительностью обслуживания заявки. Его среднее значение [секунд] называется средней длительностью обслуживания, а обратная к ней величина называется интенсивностью обслуживания.

Если C постоянно, то можно не делать различия между длиной заявки и длительностью ее обслуживания и в этом случае будем полагать, что . Тем самым длина заявки измеряется в единицах времени. Это соглашение принимается всюду далее, если не оговорено противное.

Пусть – длительность обслуживания k -й заявки. Если случайные величины 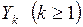независимы в совокупности, одинаково распределены и не зависят от входящего потока, то такое обслуживание называется рекуррентным. В дальнейшем, как правило, рассматриваются СМО с рекуррентным обслуживанием.

В некоторых случаях быстродействие меняется в зависимости от загрузки обслуживающего устройства. В качестве примера рассмотрим СМО с обслуживающими устройствами и общей очередью. Поступившая заявка обслуживается любым свободным обслуживающим устройством. Для простоты предположим, что все обслуживающие устройства имеют одинаковое быстродействие, скажем, C. Определим состояние СМО как число находящихся в ней заявок (как на обслуживании, так и в очереди). Тогда общее быстродействие станции обслуживания, состоящей из обслуживающих устройств, зависит от состояния и определяется формулой

.

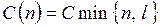Дисциплина обслуживания.

Наиболее простой и хорошо известной является дисциплина обслуживания «первый пришел – первый обслужен», при которой заявки обслуживаются полностью без прерываний в порядке их поступления, причем заявка, поступившая в момент простоя обслуживающего устройства, сразу же начинает обслуживаться. Легко представить себе ситуацию, когда эта дисциплина нежелательна. Например, часто бывает, что одни заявки важнее других и заслуживают предпочтительного обслуживания. Разделение заявок на группы по степени их важности осуществляется с помощью приоритетных дисциплин обслуживания, и соответствующая система массового обслуживания называется системой с приоритетами. Правило назначения приоритетов определяет порядок, в котором будут обслуживаться ожидающие заявки. Приоритетные дисциплины обслуживания бывают двух типов: с абсолютными приоритетами и с относительными приоритетами. Если обслуживание текущей заявки прерывается при появлении заявки с более высоким приоритетом и последняя немедленно начинает обслуживаться, то говорят, что имеет место дисциплина обслуживания с абсолютными приоритетами. Если прерывание обслуживания не допускается, то имеет место дисциплина с относительными приоритетами.

Далее, если специально не оговорено противное, рассматриваются СМО, в которых обслуживание заявок осуществляется в порядке их поступления.

Краткие обозначения. Для определения типа системы массового обслуживания часто используются обозначения вида , где символы A и B обозначают входящий поток и распределение длительности обслуживания соответственно, а l – число параллельных устройств обслуживания в СМО. Чтобы отличить СМО, в которой нет ограничений на допустимое число заявок, от СМО, в которой не может находиться более m заявок, для последней используются обозначения вида 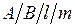. Приведем некоторые из общепринятых обозначений для часто используемых распределений:

– экспоненциальное распределение, которое приводит к “марковскому” свойству СМО;

– обозначает вырожденное распределение (deterministic), при котором интервалы между моментами поступления или моментами начала и завершения обслуживания заявок являются постоянными;

– распределение Эрланга (Erlang) k -го порядка;

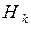– гиперэкспоненциальное (hyperexponetial) распределение k -го порядка;

– произвольное (general) распределение;

– рекуррентный входящий поток (general independent).

Таким образом, под системой понимается СМО с одним обслуживающим прибором, пуассоновским входящим потоком и экспоненциально распределенной длительностью обслуживания. Аналогично, под системой понимается СМО с одним обслуживающим устройством, рекуррентным входящим потоком и гиперэкспоненциальным распределением второго порядка длительности обслуживания.

Показатели качества. Математическая модель реальной системы строится так, чтобы оценить какие-то показатели качества этой системы. Для систем с очередями необходимо прежде всего оценить загруженность системы. Простейшей мерой загруженности является нагрузка :

 

.

 

Если величины, стоящие в числителе и знаменателе этого отношения, равны соответственно и , то .

Если нагрузка превосходит единицу, то это означает, что заявки поступают быстрее, нежели их успевает обрабатывать обслуживающее устройство. В СМО с l параллельными обслуживающими устройствами на каждое из них приходится в среднем 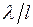заявок в единицу времени. Поэтому нагрузка в такой СМО может быть поднята в l раз.

Процесс передачи заявок в системе с одним обслуживающим устройством проиллюстрирован на рисунке.