Число заявок в системе
.
Если в каждый данный момент рассматривать значение 
как размер некоторой популяции, то 
можно интерпретировать как общее число рождений до момента времени t, а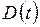 
– как число погибнувших членов популяции. Отсюда процесс можно назвать процессом рождения и гибели.
Ранее было получено:
. (1а)
Эти уравнения выполняются при 
. При 
аналогичным образом выводится уравнение
. (1б)
Если в начальный момент времени 
, то должны выполняться начальные условия 
, 
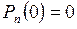при 
. Условия существования и единственности решения системы (1) отнюдь не тривиальны, и их обсуждение мы опускаем.
Мы будем искать установившееся решение системы (1), которого вполне достаточно для многих приложений. Установившееся (стационарное) решение определяется как не зависящее от t распределение вероятностей 
, 
, …, 
, удовлетворяющее системе (1). Если такое распределение существует, оно единственно и для каждого состояния n
.
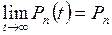Для нахождения 
можно использовать систему линейных уравнений
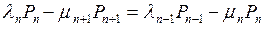, (2)
которая получается из уравнений (1а), если положить в них 
. Преобразуя уравнения системы (2), получим
, (3)
где с – постоянная. Из (1б) находим, что
.
Отсюда 
и из (3) получается следующая система рекуррентных уравнений:
(4)
Уравнению (4) можно дать следующую интерпретацию. Его левая часть представляет собой интенсивность перехода из состояния n в состояние 
, и эта величина балансируется правой частью, представляющей собой интенсивность перехода из состояния в состояние 
. Граф переходов, отвечающий уравнениям баланса (4), изображен на рис. 2.
Рис. 2. Диаграмма уравнений баланса для процесса рождения и гибели
Стационарные вероятности теперь вычисляются рекуррентно:
, (5)
где
, 
. (6)
Вероятность 
определяется из того условия, что 
, поскольку 
– распределение вероятностей. Таким образом, если ряд
(7)
Сходится, то, обозначая его сумму через 
, получим
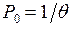. (8)
ПРОСТЕЙШАЯ СИСТЕМА 
Рассмотрим СМО с одним обслуживающим устройством, пуассоновским входящим потоком с параметром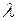 
и экспоненциально распределенной с параметром 
длительностью обслуживания. Легко видеть, что число заявок , находящихся в системе в момент времени 
, описывается процессом рождения и гибели с 
и 
. В этом случае рекуррентное соотношение (5) принимает вид
,
где 
. Если 
, то ряд сходится и
.
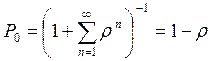Таким образом, стационарная вероятность того, что в системе находится заявок,
. (9)
Стационарное распределение (9) является геометрическим распределением. Его среднее легко вычисляется:
. (10)
Среднее время ответа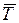 
можно легко вычислить из (10), используя первую из формул Литтла.
Среднее число заявок в системе
.
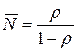Применяя первую формулу Литтла, найдем среднее время пребывания заявки в системе:
.
Найдем среднее число заявок в очереди 
. Будем рассуждать так: число заявок в очереди равно числу заявок в системе минус число заявок, находящихся на обслуживании. Значит (по правилу сложения математических ожиданий), среднее число заявок в очереди равно среднему числу заявок в системе 
минус среднее число заявок на обслуживании. Число заявок на обслуживании может быть либо нулем (если обслуживающее устройство свободно), либо единицей (если оно занято). Математическое ожидание такой случайной величины равно вероятности того, что обслуживающее устройство занято (обозначим ее 
). Очевидно, равно единице минус вероятность 
того, что обслуживающее устройство свободно:
.
Следовательно, среднее число заявок, находящихся на обслуживании, равно
,
отсюда
.
По второй формуле Литтла найдем среднее время пребывания заявки в очереди:
.
