Интенсивность потока в 
и интенсивность потока из 
в состоянии равновесия должны быть равны, поэтому
.
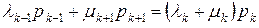Общие рассуждения о сохранении потока могут быть применены к потоку через любую замкнутую границу; например, вместо того, чтобы выделять каждое состояние и составлять для него уравнение, можно выбрать последовательность контуров, первый из которых охватывает состояние 
, второй – состояния и 
, и т. д., включая каждый раз в новую границу очередное состояние. В таком примере для k -го контура (окружающего состояния , , …, 
) условие сохранения потока можно записать в следующем простом виде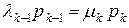 
.
Эти уравнения были выведены с помощью условия сохранения потока в состоянии 
. Член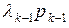 
в левой части равен члену 
в правой части равенства. Это точно описывает метод локального равновесия, который именно в том и состоит, чтобы найти в системе глобального равновесия подмножество членов, между которыми существует равновесие и которые приводят к системе уравнений локального равновесия.
Важно заметить, что если речь идет об эргодическом марковском процессе, то можно с уверенностью сказать, что имеется единственное стационарное распределение вероятностей. Затем, если для такого процесса систему уравнений глобального равновесия разложить на множество более мелких систем уравнений локального равновесия, содержащих согласованные члены из глобальной системы (и, конечно, учитывающих все члены глобальной системы), то любое решение, удовлетворяющее системам уравнений локального равновесия, должно также удовлетворять системе уравнений глобального равновесия; обратное утверждение в общем случае неверно. Таким образом, любое решение системы уравнений локального равновесия должно приводить к единственному решению, описывающему рассматриваемый марковский процесс.
В интересующем нас случае сети массового обслуживания определим систему уравнений локального равновесия (соответствующую заданному состоянию сети и заданному узлу i) как систему, в которой приравнивается интенсивность потока из данного состояния сети за счет ухода требований из узла i к интенсивности потока в данное состояние сети за счет поступления требований в узел i. Это понятие для сетей лучше всего проиллюстрировать простым примером, показанным на рисунке.
Пример простой циклической сети (N = 3; K = 2)
Здесь представлена сеть с тремя узлами: интенсивность обслуживания в i -м узле равна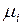 
и не зависит от числа требований в нем. Предполагается, что по этой замкнутой циклической сети циркулируют точно 
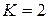требований. Очевидно, что 
и 
в остальных случаях. Состояния сети описываются тройками 
, где 
- число требований в узле i; в рассматриваемом случае 
. Таким образом, для рассматриваемой сети имеется точно 6 состояний; интенсивности переходов между этими состояниями показаны на следующем рисунке
