Фінансовою рентою або ануїтетом називається ряд послідовних фіксованих платежів, що виконуються через рівні проміжки часу.
Фінансові ренти (ануїтети) характеризуються такими параметрами:
1) член ренти - величина кожного окремого платежу;
2) період ренти - часовий інтервал між двома платежами;
3) термін ренти - час від початку реалізації ренти до моменту нарахування останнього платежу;
4) процентна ставка - ставка, що використовується для розрахунку нарощування платежів, складових ренту.
Крім того, рента характеризується: кількістю платежів в рік, частотою нарахування відсотків, моментом виробництва платежу (на початку, середині або в кінці року) і так далі.
Узагальнюючими показниками ренти (ануїтету) є майбутня (нарощена) і поточна або справжня (приведена) її величина.
Майбутня вартість ануїтету - це сума всіх членів потоку платежів з нарахованими на них відсотками на кінець терміну, тобто на дату останньої виплати.
Для визначення майбутньої вартості звичайного ануїтету можна використовувати формулу:
 (49)
(49)
де F - майбутня вартість звичайного ануїтету;
C - величина щорічного внеску (платежу);
T - термін ануїтету;
n - процентна ставка;
 - коефіцієнт нарощування ануїтету.
- коефіцієнт нарощування ануїтету.
У практиці фінансових розрахунків з використанням ануїтетів можуть бути різні варіанти рентних платежів і нарахування відсотків. Розглянемо 4 можливих варіантів ануїтетів.
1. Рентні платежі вносяться раз на рік, а відсотки на них нараховуються кілька разів на рік, наприклад, (m) разів на рік. В цьому випадку майбутня вартість ануїтету визначається по формулі:
 (50)
(50)
2. Рентні платежі вносяться кілька разів протягом року рівними сумами, а нарахування відсотків проводиться один раз в кінці року. За таких умов майбутня вартість ануїтету може бути визначена:
 , (51)
, (51)
де р — число рентних платежів протягом року.
3. Рентні платежі вносяться (р) раз на рік, нарахування відсотків проводиться (m) раз на рік, число періодів нарахування відсотків протягом року рівне числу рентних платежів і перебіг року, тобто m = р. В цьому випадку майбутня вартість ануїтету визначається по формулі:

де n - номінальна ставка відсотків;
t - термін ренти в роках;
m - число періодів нарахування відсотків протягом року.
Рентні платежі вносяться (р) раз на рік, нарахування відсотків проводиться (m) раз на рік, число рентних платежів дорівнює числу періодів нарахування відсотків, тобто р ≠ m. Майбутня вартість ануїтету може бути визначена з формули:
 , (53)
, (53)
де р - число рентних платежів протягом року;
m - число періодів нарахування відсотків протягом року;
n - номінальна процентна ставка;
t - термін ренти.
Приклад 24. Рентні платежі виплачуються протягом 5 років у розмірі 10 тис. грн. Процентна ставка 12% річних. Визначити майбутню вартість ануїтету за наступних умов:
а) платежі вносяться один раз до року, а відсотки нараховуються щоквартально;
б) платежі вносяться 2 рази до року рівними сумами, а відсотки нараховуються один раз в рік;
в) рентні платежі вносяться щоквартально, відсотки нараховуються щоквартально;
г) рентні платежі вносяться щокварталу, а відсотки нараховуються по півріччям.
Рішення: Використовуємо формули 50, 51, 52, 53
а) F = 10 х ((1 + 0,12 / 4)5х4 -1)/(1 + 0,12 /4)4-1) = 64,227 тис. грн.
б) F = 10 х ((1 + 0,12)5 -1) /(2 х ((1 + 0,12)1/2 -1)) = 65,380 тис. грн.
в) F = 10 х ((1 + 0,12 /4)5х4-1)/ 0,12 = 67,176 тис. грн.
г) F = 10 х ((1 + 0,12 / 2)5х2 -1) /(4 х ((1 + 0,12 / 2)2/4 -1)) = 66,878 тис. грн.
При здійсненні фінансових обчислень іноді виникає необхідність визначення розмірів разових платежів і терміну ануїтету.
Величина рентного платежу може бути визначена по формулі:
 (54)
(54)
Термін ануїтету визначається по формулі:
 (55)
(55)
Справжня величина потоку рентних платежів - це сума всіх його членів, зменшена (дисконтована) на величину процентної ставки на певний момент часу, співпадаючий з початком потоку платежів, або передуючий йому.
Справжня величина показує, яку суму необхідно мати спочатку, щоб, розбивши її на рівні внески, на які б нараховувалися встановлені відсотки протягом терміну ренти, можна було забезпечити отримання нарощеної суми.
Оцінка справжньої величини проводиться на момент початку реалізації ренти.
Для ренти з членами, рівними (С), справжня величина визначається по формулі:
 (56)
(56)
де А — справжня величина потоку рентних платежів;
С — сума рентного платежу;
а — коефіцієнт приведення ренти, що показує, скільки рентних платежів (С) міститься в справжній величині.
Коефіцієнт приведення ренти (а) визначається по формулі:
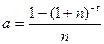 (57)
(57)
Приклад 25. Сім'я бажає протягом 3 років зібрати суму для придбання автомобіля вартістю 95 тис. грн. Вона може виділити на ці цілі 28 тис. грн. щорічно, поміщаючи їх в банк під 12,5% річних (відсотки складні). Яка сума була б потрібна сім'ї для придбання автомобіля вартістю 95 тис. грн., якби суму, що необхідна, помістили в банк на 3 роки під 12,5% річних?
Рішення: С=28 тис. грн., t=3; n=12,5%.
 тис. грн.
тис. грн.
Дійсно, якби сім'я мала можливість вказану суму (66,678 тис. грн.) помістити в банк на три роки під 12,5% річних, то нарощена сума склала б:
F = 66,678 х (1 + 0,125)3 = 94,938 тис. гр. ≈ 95 тис. грн.
Нарощена сума при щорічних платежах у розмірі 28 тис. грн. під 12,5% річних складе:
 тис. грн.
тис. грн.
З цього прикладу можна вивести математичний взаємозв'язок величин:

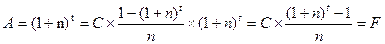 (58)
(58)
або

 (59)
(59)
Контрольні питання:
1. Визначте сутність оцінки вартості грошей в часі.
2. Надайте класифікацію відсоткових ставок.
3. Окресліть завдання щодо визначення зміни вартості грошей у часі.
4. Розкрийте сутність використання майбутньої вартості грошей у фінансових розрахунках.
5. Надайте характеристику визначення теперішньої вартості грошей у фінансових розрахунках.
6. Виділіть основні методи нарахування відсотків.
7. Розкрийте методику визначення майбутньої вартості грошей з урахуванням інфляційного чинника.
8. Охарактеризуйте сутність і основні параметри ануїтету та порядок визначення його майбутньої вартості.






