Справжня вартість грошей - це сума, що отримується в результаті приведення майбутньої вартості грошей до справжнього моменту за допомогою дисконтної ставки.
Якщо припустити, просту фінансову операцію, в результаті якої майбутня вартість засобів (F) приводиться до деякої справжньої суми (Р), то така операція характеризується показником, що називається темпом зниження (і(t)):
(36)
Темп зниження прийнято називати коефіцієнтом дисконтування або дисконтною ставкою.
Приклад 17. Підприємство повинне повернути в банк суму довга у розмірі 500 тис. грy. Справжня приведена сума кредиту, взятого на один рік, склала 400 тис. грн. Визначити коефіцієнт дисконтування або дисконтну ставку.
Рішення: Використовуємо формулу 36
або 20%
Метод дисконтування найчастіше використовується в операціях по обліку векселів і оцінки ефективності інвестиційних проектів.
Облік векселя - це рішення банку купити вексель у векселедержателя.
У теорії фінансових обчислень існують два методи розрахунку справжньої вартості: математичний і банківський (комерційний).
При математичному методі визначення справжньої вартості використовується процентна дисконтна ставка, тобто вирішується завдання зворотнє визначенню нарощеної суми. Це завдання, формулюється таким чином: яку суму грошей слід дати у борг на термін (t) років, щоб при нарахуванні на неї відсотків по ставці (n) отримати нарощену величину, рівну (F).
Банківський метод визначення справжньої вартості заснований на використанні облікової ставки (d), тобто відсотки за користування позикою нараховуються на суму, що підлягає сплаті в кінці терміну позики.
Визначення справжньої вартості грошей при математичному методі припускає використання схем простої і складної дисконтної ставки.
Справжня вартість грошей при використанні простої дисконтної ставки визначається по формулі:
, (37)
де Р - проста процентна дисконтна ставка;
t - термін фінансової операції (число повних років); у випадку коли (t) менше 1 року, тоді 
(f - число днів операції або число днів обернення векселя, або число днів до дати погашення векселя, або число місяців руху векселя; k - тривалість року в днях або в місяцях - 365(366) днів або 12 місяців):
F - майбутня вартість грошей (майбутня або номінальна вартість векселя).
Дисконт визначається по формулі:
, (38)
Приклад 18. Банк видав вексель строком на 1 рік, по якому можна буде отримати суму, 250 тис. грн. Яка була внесена до банку сума грошей у момент придбання векселя, якщо його прибутковість повинна скласти 11% річних?
Рішення: Використовуємо формулу 37
тис. грн.
Приклад 19. Власник векселя номінальною вартістю 250 тис. грн. і терміном обернення 1 рік надав його банку - емітенту для обліку за 120 днів до дати погашення. Банк врахував вексель по ставці 16% річних. Визначити суму, що отримана власником векселя і величину дисконту, отриману банком.
Рішення: Використовуємо формули 37 і 38
тис. грн.
тис. грн.
Справжня вартість грошей при використанні складної процентної дисконтної ставки визначається по формулі:
, (39)
| де |
- дисконтний множник;
і - складна процентна дисконтна ставка.
У фінансових обчисленнях базова формула (4.39) визначення справжньої вартості може бути трансформована з урахуванням різних періодів формування грошових потоків:
(40)
де F1, F2, F3, …Ft - майбутня вартість грошей, що формується по періодах;
(1 +i)1, (1 +i)2, (1 +i)3 , …, (1 +i)t - дисконтні множники по періодах;
t - число періодів, приведення майбутньої вартості до справжнього моменту часу.
Запропонована формула є базовою для оцінки ефективності інвестиційних проектів. Щоб оцінити ефективність інвестиційного проекту у формулу 40 необхідно внести невеликі доповнення, що припускають зменшення справжньої приведеної вартості на величину стартових інвестицій. Формула для розрахунку може бути:
, (41)
де NPV – чиста приведена вартість;
ІС - стартові інвестиції.
Приклад 20. Підприємство прогнозує реалізувати інвестиційний проект вартість в 1 млн. грн. базових інвестицій протягом одного року. Дисконтна процентна ставка встановлена за проектом на рівні 12% річних. Чистий поворотний грошовий потік формується протягом 5 років. У перший рік чистий поворотний потік складе 160 тис. грн., у другому році - 390 тис. грн., у третьому році 560 тис. грн., у четвертому році - 490 тис. грн., у п'ятому році - 350 тис. грн. Оцінити ефективність інвестиційного проекту, розрахувавши його справжню приведену вартість і суму дисконту за даним проектом.
Рішення: Використовуємо формулу 41
Оскільки отримана сума позитивна, то даний інвестиційний проект можна визнати як економічно ефективний. Проте для остаточного вирішення потрібний підрахунок і ряду інших показників, наприклад, періоду або терміну окупності і тому подібне.
При нарахуванні складних дисконтних відсотків (m) раз на рік формулу 39 можна представити у такому вигляді:
, (42)
де 
- дисконтний множитель.
Для формул 39 і 42 значення дисконту може бути визначено по наступним формулам:
, (43)
, (44)
Приклад 21. Визначити справжню вартість суми 120 тис. грн., яку повинні виплатити через 3 роки, якщо на первісну суму нараховувалися складні відсотки в розмірі 12% річних. Додаткові умови: а) нарахування проводилося 1 раз на рік; б) нарахування проводилося щокварталу.
Рішення: Використовуємо формули 39 і 42
а) 
тис. грн.
б) 
тис. грн.
При банківському методі визначення справжньої приведеної вартості грошей при простій обліковій дисконтній ставці розрахунок проводиться по формулі:
(45)
де d - облікова дисконтна ставка, долі одиниць.
Задача 22. Векселедержатель надав для обліку вексель на суму 3 млн. грн. з терміном погашення 1 лютого поточного року. Вексель пред'явлено 12.01 поточного року. Банк погодився врахувати вексель з дисконтом 14% річних. Визначити суму, яку отримає векселедержатель і суму дисконту, отриману банком.
Рішення: Використовуємо формулу 45
тис. грн. (отримав векселедержатель).
тис. грн.(сума дисконту).
Задача 23. Підприємство продало товар в кредит з оформленням простого векселя, номінальна вартість якого 450 тис. грн., термін векселя - 60 днів, ставка відсотка за кредит - 19% річних. Через 45 днів з моменту оформлення векселя підприємство вирішило врахувати вексель в банку; запропонована банком дисконтна ставка склала 15% річних. Визначити суми, отримані підприємством і банком в результаті даної операції.
Рішення:
а) визначимо майбутню вартість векселя до моменту його погашення:
тис. грн.
б) визначимо термінову вартість векселя у момент обліку його банком:
тис. грн..
в) визначимо суму, яку отримає підприємство:
тис. грн.
г) визначимо суму грошей, яку отримає банк за 15 днів до погашення векселя:
464,055 - 460,541 = 3,514 тис. грн.
д) визначимо суму комісійних, отриманих банком при обліку векселя:
460,541 - 455,473 = 5,068 тис. грн.
е) загальна сума коштів, отримана банком при обліку векселю:
3,514 + 5,068 = 8,582 тис. грн.
Справжня вартість грошей при складній дисконтній обліковій ставці визначається по формулі:
(46)
де d - складна річна дисконтна облікова ставка.
Дисконт обчислюється за формулою:
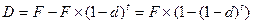(47)
Складна дисконтна облікова ставка може бути визначена по формулі:
(48)
