Подобно тому, как в трубной гидравлике критерием режима движения служит число Рейнольдса
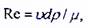(5,1)
в теории фильтрации вводится безразмерный параметр
(5,2)
где и - некоторая характерная скорость; а - линейный параметр, характеризующий среднее сечение поровых каналов; ρ - плотность жидкости; μ - динамический коэффициент вязкости.
Скорость фильтрации, при которой нарушается закон Дарси, называется критической скоростью фильтрации (ώкр).
Однако нарушение линейного закона фильтрации еще не означает перехода от ламинарного движения к турбулентному. Закон Дарси нарушается вследствие того, что силы инерции, возникающие в жидкости за счет извилистости каналов и изменения площади их поперечных сечений, становятся при ώ> ώкр соизмеримыми с силами трения.
В трубной гидравлике значение Re, при котором происходит смена режимов, равно Reкр= 2320, в теории фильтрации закон Дарси имеет место при значении безразмерного параметра Re, меньшего критического (Reкр), которое устанавливается из опыта.
Впервые число Рейнольдса для фильтрации жидкости было введено Н.Н.Павловским в виде
(5,3)
т. е. за характерную скорость была взята скорость фильтрации со, а линейный параметр представлен выражением
(5,4)
Критические значения Re по Павловскому заключены в интервале
В.Н.Щелкачев предложил взять за линейный параметр выражение, пропорциональное корню квадратному из коэффициента проницаемости,
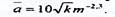(5.5)
Число Рейнольдса по В.Н.Щелкачеву имеет вид
(5,6)
а критические значения лежат в интервале
По М.Д.Миллионшикову за характерную скорость взята средняя скорость движения жидкости
а за линейный параметр – выражение 
,т.е
0,022 < Reкр< 0,29.
Если вычисленное по одной из формул (5.3), (5.6), (5.7) значение числа Re оказывается меньше нижнего критического значения Reкр , то закон Дарси справедлив, если Re больше верхнего значения Reкр, то закон Дарси заведомо нарушен.
Широкий диапазон изменения Reкр объясняется тем, что формулы для числа Re входят параметры k и т. которые не полностью характеризуют микроструктуру породы. Как следует из опытов, для каждой горной породы можно указать более узкий диапазон значений Reкр.
Определение режима фильтрации жидкостей и газов имеет большое практическое значение, ибо без знания закона фильтрации в пласте нельзя правильно рассчитать дебиты скважин, распределение давления в пласте, а также невозможно определение параметров пласта (k, h, т и др.) по данным исследования нефтяных и газовых скважин.
При нарушении закона Дарси зависимость между скоростью фильтрации ώ и градиентом давления dp /ds лучше всего описывается двучленной формулой
(5,8)
которая выражает плавный переход от линейного закона фильтрации к нелинейному. При малых значениях скорости aώ>>b ώ2 пренебрегаем вторым членом и получаем закон Дарси; при значениях,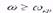 
слагаемые aώ и b ώ2 имеют один и тот же порядок; при больших скоростях фильтрации aώ<<b ώ2 и можно принять
(5,9)
что соответствует квадратичному закону сопротивления и имеет место при фильтрации в крупнозернистых и трещиноватых породах. Формула (5.9) называется формулой А.А. Краснопольского.
Коэффициенты a и b определяются либо экспериментально, либо а по формуле a=μ/k, а b- приближенно по формуле, предложенной А.И. Ширковским
(5.10)
где р - плотность в кг/м3; k - коэффициент проницаемости в мкм2; т - коэффициент пористости в долях единицы.
Можно записывать закон фильтрации, отличный от закона Дарси, в виде одночленной степенной зависимости между скоростью фильтрации и градиентом давления:
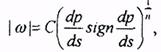(5,11)
где sign - знак производной dp/ds; С и n- некоторые постоянные, определяемые опытным путем, причем 1<п<2, п-2 соответствует закону Краснопольского.
Используя принцип однородности размерностей, можно найти выражение для коэффициента С:
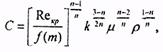(5,12)
где ƒ(m)=10m-2.3
Задача 1
Определить значение числа Рейнольдса у стенки гидродинамически несовершенной по характеру вскрытия нефтяной скважины, если известно, что
эксплуатационная колонна перфорирована, на каждом метре длины колонны прострелено 10 отверстий диаметром d0=10 мм, толщина пласта h=I5 м, проницаемость пласта k=1 мкм2, пористость его m=18%, коэффициент вязкости нефти μ=4 мПа*с, плотность нефти ρ = 870 кг/м3 и дебит скважины составляет 140 м3/сут.
Задача 2
Определить радиус призабойной зоны rкр, в которой нарушен закон Дарси, при установившейся плоскорадиальной фильтрации идеального газа, если известно, что приведенный к атмосферному давлению дебит скважины Qатт=2*10 м3/сут, толщина пласта h=10 м, коэффициент проницаемости k=0,6 мкм2, коэффициент пористости пласта μ =19%, динамический коэффициент вязкости газа в пластовых условиях μ =1,4*10'2 мПа*с, плотность газа при атмосферном давлении и пластовой температуре ρ =0,7 кг/м3.
Указание. В решении использовать число Рейнольдса по формуле М.Д. Миллионщикова и за Reкp взять нижнее значение Reкp =0,022.
Задача 3
Определить по формуле Щелкачева, происходит ли фильтрация в пласте по закону Дарси, если известно, что дебит нефтяной скважины Q=200 м3/сут, толщина пласта h=5 м, коэффициент пористости m=16%, коэффициент проницаемости k=0,2 мкм2, плотность нефти ρ =0,8 г/см3,
динамический коэффициент вязкости ее μ=5 мПа*с. Скважина
гидродинамически совершенна, радиус ее rс=0,1 м.
